
Machine
Learning
Joern Ploennigs
Datenvorverarbeitung
Fehlende Beobachtungen¶
In vielen Datensätzen aus der Praxis stoßen wir auf fehlende Werte. Sie enstehen weil (i) Werte nicht regelmäßig erfasst wurden, (ii) Werte historisch nicht gemessen wurden, (iii) Messgeräte ausfallen oder (iv) Werte entfernt worden sind, weil man dachte, dass sie nicht benötigt werden.
Solche fehlenden Werte, können sehr schnell Berechnungen verfälschen oder unmöglich machen. Zum Beispiel, meldet ein Temperatursensor auf einer Brücke im Fehlerfall -9999. Wird dieser Wert bei der Mittelwertbildung nicht erkannt, könnte er die statistische Analyse verfälschen. Deshalb ist es wichtig, fehlende Werte zu identifizieren und diese richtig zu behandeln.
Wie werden fehlende Daten codiert?¶
Grundsätzlich ist es wichtig das man fehlende Werte in den Daten codiert und abspeichert, denn nur so kann man unterscheiden, ob sie bewusst oder zufällig fehlen.
| Sprache / Tool | Fehlender Wert |
|---|---|
| Python (NumPy) | np.nan |
| Python (Pandas ab v1.0) | pd.NA |
| R | NA |
| Julia | missing |
| Excel | Leeres Feld |
| Geräte | -9999, 99999 o.ä. |
Dabei unterscheidet sich auch die Bedeutung der Codierung. In Numpy steht np.nan eigentlich für "Not a Number". In Pandas steht pd.NA für "Not Available" und ist eindeutiger als np.nan. Diese Vielfalt macht es notwendig, sich immer die Datendokumentation anzusehen.
Umgang mit fehlenden Werten¶
Um den Umgang mit fehlenden Werten zu lernen, schauen wir uns den Wetter Datensatz des DWD für die Wetterstation in Warnemünde vor 1960 an.
import numpy as np # Import von NumPy
import pandas as pd # Import von Pandas
np.random.seed(3) # Fixierung des Zufallszahlgenerators zur beseren Erklärung
wetter = pd.read_csv("../data/Wetter/warnemuende_1960.csv", sep=';')
wetter.shape
(7209, 19)
Die Originaldaten enthalten {glue}:wetter_size1 Zeilen und {glue}:wetter_size2 Spalten.
Als erstes schauen wir uns die Daten mal an. Hierfür bieten sich die *.head() und *.tail() Funktionen, da sie uns den Anfang und das Ende des Datensatzes zeigen.
wetter.head()
| STATIONS_ID | MESS_DATUM | QN_3 | FX | FM | QN_4 | RSK | RSKF | SDK | SHK_TAG | NM | VPM | PM | TMK | UPM | TXK | TNK | TGK | eor | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 4271 | 19470101 | -999 | -999 | -999.0 | 5 | -999.0 | -999 | -999.0 | -999 | -999.0 | 4.1 | 1019.3 | -2.1 | 78.0 | -1.5 | -3.3 | -5.8 | eor |
| 1 | 4271 | 19470103 | -999 | -999 | -999.0 | 3 | -999.0 | -999 | -999.0 | -999 | -999.0 | 3.6 | 1032.4 | -4.8 | 80.0 | -2.4 | -6.2 | -4.5 | eor |
| 2 | 4271 | 19470105 | -999 | -999 | -999.0 | 5 | -999.0 | -999 | -999.0 | -999 | -999.0 | 1.9 | 1031.9 | NaN | 79.0 | -9.4 | -14.0 | -16.0 | eor |
| 3 | 4271 | 19470108 | -999 | -999 | -999.0 | 5 | -999.0 | -999 | -999.0 | -999 | -999.0 | 1.9 | 1023.1 | NaN | 82.0 | -9.8 | -15.3 | -19.0 | eor |
| 4 | 4271 | 19470109 | -999 | -999 | -999.0 | 5 | -999.0 | -999 | -999.0 | -999 | -999.0 | 2.4 | 1017.5 | NaN | 84.0 | -8.7 | -13.7 | -19.0 | eor |
Als erstes schauen wir uns die Daten mal an. Hierfür bieteten sich die head und tail Funktionen, da sie uns den Anfang und das Ende des Datensatzes zeigen.
wetter.tail()
| STATIONS_ID | MESS_DATUM | QN_3 | FX | FM | QN_4 | RSK | RSKF | SDK | SHK_TAG | NM | VPM | PM | TMK | UPM | TXK | TNK | TGK | eor | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7204 | 4271 | 19660926 | 5 | -999 | 6.6 | 5 | 0.3 | 1 | 2.2 | 0 | 6.6 | 12.8 | 1014.0 | 13.1 | 86.0 | 15.1 | 9.5 | 7.9 | eor |
| 7205 | 4271 | 19660927 | 5 | -999 | 10.0 | 5 | 0.0 | 1 | 6.1 | 0 | 5.8 | 10.1 | 1014.3 | 12.0 | 72.0 | 13.3 | 10.9 | 10.4 | eor |
| 7206 | 4271 | 19660928 | 5 | -999 | 4.5 | 5 | 0.0 | 0 | 9.9 | 0 | 2.6 | 9.1 | 1017.5 | 9.7 | 74.0 | 12.5 | 7.7 | 8.7 | eor |
| 7207 | 4271 | 19660929 | 5 | -999 | 3.3 | 5 | 0.0 | 0 | 7.8 | 0 | 4.8 | 9.2 | 1015.8 | 9.7 | 78.0 | 14.9 | 5.1 | 3.1 | eor |
| 7208 | 4271 | 19660930 | 5 | -999 | 3.5 | 5 | 0.0 | 0 | 7.8 | 0 | 2.2 | 10.9 | 1007.9 | 11.1 | 83.0 | 16.1 | 5.8 | 4.8 | eor |
Es gibt also am Anfang des Datensatzes sehr viele Werte die -999 oder -999.0 sind. Am Ende allerdings nur noch in der Spalte FX. Wir können also davon ausgehen, dass in dem Datensatz fehlende Werte mit -999 codiert worden sind. Die fehlenden Werte sind auch erklärbar, da 1947 Messungen noch händisch durchgeführt wurden und nur einfache Größen wie Temperatur erfasst wurden.
Diese fehlenden Werte müssen wir mit np.nan oder pd.NA ersetzen. Hierfür können wir die Dataframe-Methode replace an.
wetter = wetter.replace(-999, pd.NA)
wetter.head()
| STATIONS_ID | MESS_DATUM | QN_3 | FX | FM | QN_4 | RSK | RSKF | SDK | SHK_TAG | NM | VPM | PM | TMK | UPM | TXK | TNK | TGK | eor | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 4271 | 19470101 | <NA> | <NA> | <NA> | 5 | <NA> | <NA> | <NA> | <NA> | <NA> | 4.1 | 1019.3 | -2.1 | 78.0 | -1.5 | -3.3 | -5.8 | eor |
| 1 | 4271 | 19470103 | <NA> | <NA> | <NA> | 3 | <NA> | <NA> | <NA> | <NA> | <NA> | 3.6 | 1032.4 | -4.8 | 80.0 | -2.4 | -6.2 | -4.5 | eor |
| 2 | 4271 | 19470105 | <NA> | <NA> | <NA> | 5 | <NA> | <NA> | <NA> | <NA> | <NA> | 1.9 | 1031.9 | NaN | 79.0 | -9.4 | -14.0 | -16.0 | eor |
| 3 | 4271 | 19470108 | <NA> | <NA> | <NA> | 5 | <NA> | <NA> | <NA> | <NA> | <NA> | 1.9 | 1023.1 | NaN | 82.0 | -9.8 | -15.3 | -19.0 | eor |
| 4 | 4271 | 19470109 | <NA> | <NA> | <NA> | 5 | <NA> | <NA> | <NA> | <NA> | <NA> | 2.4 | 1017.5 | NaN | 84.0 | -8.7 | -13.7 | -19.0 | eor |
Alternativ können wir die Daten direkt aus der CSV mit NA Werten laden, indem wir den Parameter na_values angeben.
wetter = pd.read_csv("../data/Wetter/warnemuende_1960.csv", sep=';', na_values=['-999','NA'])
Jetzt haben wir einen Datensatz, in dem die fehlenden Werte richtig codiert sind. Jetzt ist es sinnvoll zu evaluieren, wie viele Daten fehlen. Wir können mit der Methode count beginnen: Diese Methode gibt die Anzahl der gültigen Beobachtungen für ein Dataframe oder eine einzelne Variable an. Und "gültig" bedeutet hier alles außer np.nan. Die Anzahl der gültigen Beobachtungen für jede Variable ist:
wetter.count()
STATIONS_ID 7209 MESS_DATUM 7209 QN_3 4656 FX 0 FM 4656 QN_4 7209 RSK 5752 RSKF 5752 SDK 5752 SHK_TAG 5752 NM 5752 VPM 7209 PM 7209 TMK 7209 UPM 7209 TXK 7209 TNK 7209 TGK 7209 eor 7209 dtype: int64
Wir können sehen, dass einige Variablen, z.B. TNK und TGK, gültige Werte für alle {glue}:wetter_size1 Fälle haben, während FX keinen einzigen gültigen Werte hat.
Alternativ können wir die Anzahl der fehlenden Werte direkt zählen. Hierfür können wir zwei Methoden kombinieren: isna (oder isnull) gibt für jede Beobachtung an, ob sie fehlt (wahr oder falsch), und sum addiert diese Wahrheitswerte und Falschwerte, wobei Wahrheitswerte in Einsen und Falschwerte in Nullen umgewandelt werden. Auf diese Weise kann dieser Ansatz wie count die Anzahl der fehlenden Werte für jede Variable in einem Dataframe oder nur für eine einzelne Variable in einer Serie produzieren. So können wir die Anzahl der fehlenden Werte wie folgt erhalten:
wetter.isna().sum()
STATIONS_ID 0 MESS_DATUM 0 QN_3 2553 FX 7209 FM 2553 QN_4 0 RSK 1457 RSKF 1457 SDK 1457 SHK_TAG 1457 NM 1457 VPM 0 PM 0 TMK 0 UPM 0 TXK 0 TNK 0 TGK 0 eor 0 dtype: int64
Offensichtlich können wir das gleiche Ergebnis erzielen, indem wir die Anzahl gültigen Werte von der Anzahl der Zeilen abziehen
wetter.shape[0] - wetter.count()
STATIONS_ID 0 MESS_DATUM 0 QN_3 2553 FX 7209 FM 2553 QN_4 0 RSK 1457 RSKF 1457 SDK 1457 SHK_TAG 1457 NM 1457 VPM 0 PM 0 TMK 0 UPM 0 TXK 0 TNK 0 TGK 0 eor 0 dtype: int64
Diese beiden Beispiele zeigen count und isna, die auf Dataframes angewendet werden. Wenn wir nur die Anzahl der fehlenden Werte in einer einzelnen Variablen zählen wollen, können wir einfach diese Variable auswählen. Zum Beispiel auf die Spalte QN_3:
wetter.QN_3.count()
4656
Ein guter Weg, um fehlende Beobachtungen zu entfernen, ist die Verwendung der Methode dropna. Standardmäßig werden alle Zeilen entfernt, die einen fehlenden Wert enthalten.
t = wetter.dropna()
t.shape
(0, 19)
Wir haben keine Beobachtungen mehr! Es gibt keine einzige Zeile, die gültige Werte in allen Zellen hat. Während dieser Fehler hier leicht zu erkennen ist---da nachfolgende Analysen ohne Werte scheitern werden---können solche Probleme insbesondere bei großen Datensätzen und in automatisierten Datenanalyseverfahren zu Fehlern und falschen Ergebnissen führen, die nicht augenscheinlich falsch sind. Stellen Sie sich den Fall vor, dass das Entfernen von fehlenden Werten unseren Datensatz um 90 % verkleinert, weil eine irrelevante Variable größtenteils fehlt. Es sei denn, wir überprüfen die resultierende Anzahl von Zeilen, könnten wir unsere Analyse auf einem völlig falschen Subset abschließen.
Wie die obigen Tabellen nahelegen, ist der Hauptverursacher die Spalte FX die keine einzigen gültigen Wert enthält. In solchen Fällen ist es sinnvoll solche Spalten komplett zu entfernen. Dies können wir auch mit der Methode dropna machen, indem wir sie nur auf Spalten anwenden (axis=1) und diese entfernen, wenn alle Werte darin fehlen (how="all"):
t = wetter.dropna(axis=1, how="all")
t.shape
(7209, 18)
Wenn unsere Analyse nur bestimmte Variablen erfordert, sollten wir nicht alle solchen Zeilen entfernen, sondern nur diejenigen Zeilen entfernen, in denen unsere wichtigen Variablen fehlen. Wollen wir z.B. nur die Temperatur (TMK) und Luftfeuchtigkeit (UPM) analysieren, können wir die fehlenden Zeilen nur in diesen beiden Variablen entfernen, indem wir das Argument subset verwenden:
w = t.dropna(subset=["TMK", "UPM"])
w.shape
(7209, 18)
w.head()
| STATIONS_ID | MESS_DATUM | QN_3 | FM | QN_4 | RSK | RSKF | SDK | SHK_TAG | NM | VPM | PM | TMK | UPM | TXK | TNK | TGK | eor | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 4271 | 19470101 | NaN | NaN | 5 | NaN | NaN | NaN | NaN | NaN | 4.1 | 1019.3 | -2.1 | 78.0 | -1.5 | -3.3 | -5.8 | eor |
| 1 | 4271 | 19470103 | NaN | NaN | 3 | NaN | NaN | NaN | NaN | NaN | 3.6 | 1032.4 | -4.8 | 80.0 | -2.4 | -6.2 | -4.5 | eor |
| 2 | 4271 | 19470105 | NaN | NaN | 5 | NaN | NaN | NaN | NaN | NaN | 1.9 | 1031.9 | -12.9 | 79.0 | -9.4 | -14.0 | -16.0 | eor |
| 3 | 4271 | 19470108 | NaN | NaN | 5 | NaN | NaN | NaN | NaN | NaN | 1.9 | 1023.1 | -12.9 | 82.0 | -9.8 | -15.3 | -19.0 | eor |
| 4 | 4271 | 19470109 | NaN | NaN | 5 | NaN | NaN | NaN | NaN | NaN | 2.4 | 1017.5 | -9.9 | 84.0 | -8.7 | -13.7 | -19.0 | eor |
Wenn unsere Analyse nur bestimmte Variablen erfordert, sollten wir nicht alle solchen Zeilen entfernen, sondern nur diejenigen Zeilen entfernen, in denen unsere wichtigen Variablen fehlen. Stellen Sie sich vor, wir möchten die Variablen age und home.dest analysieren. Wir können die fehlenden Zeilen nur in diesen beiden Variablen entfernen, indem wir das Argument subset verwenden:
Falsche Beobachtungen¶
Bisher haben wir diskutiert, wie wir mit fehlenden Werten umgehen. Es gibt darüber hinaus weitere Gründe für fehlerhafte und ungewöhnliche Daten, wie Messfehler, Eingabefehler, Einheitenfehler, Skalierungsfehler, Berechnungsfehler, etc. Diese Werte könne Ergebnisse sehr stark verzerren. Deshalb ist es wichtig sie zu identifizieren und zu behandeln. Man unterscheidet die folgenden Arten:
- Fehlende Werte: Sind Werte bei denen bekannt ist, dass sie fehlen.
- Außerhalb des Wertebereichs (Out-of-range): Sind Werte die logisch ausschließbar sind. Zum Beispiel weil sie außerhalb des definierten Wertebereichs liegen (z.B. Temperatur < -273.15°C), außerhalb des Messbereichs liegen (z.B. Raumtemperatursensor > 60°C), oder offensichtlich Falsch sind (z.B. 200 Jahre alter Mensch).
- Ausreißer: Sind Werte, die statistisch deutlich von den restlichen Daten abweichen. Sie können entweder viel größer oder viel kleiner sein als die meisten anderen Werte. Sie sind insbesondere dann ein Problem, wenn sie häufiger auftreten als statistisch erklärbare Werte.
- Anomalien: Sind Werte, die Kausal erklärbar sind, aber vom erwarteten Verhalten abweichen, z.B. Wetteranomalien.
Diese fehlerhaften oder ungewöhnlichen Werte werden meist unterschiedlich behandelt:
- Werte außerhalb des Wertebereichs werden meist als fehlende Werte codiert und genauso behandelt, weil sie ja nicht erklärbar auftreten können.
- Die Behandlung von Ausreißer ist schwieriger, da sie statistisch vorkommen können und somit erklärbar wären. Man behandelt sie meist nur dann, wenn sie statistisch ungewöhnlich häufig auftreten (ein Indiz für Fehler) oder aber z.B. beim Berechnen von stabilen ML-Modellen stören, da sie sehr starke Varianzen erzeugen.
- Anomalien sind ungewöhnlich, aber erklärbar und häufig ist es ein Ziel von ML-Modellen diese zu identifizieren (Anomalierkennung). Deshalb entfernt man sie nur selten, wenn man anomaliefreie Datensätze braucht, um ML-Modelle zu trainieren die das Normalverhalten vorhersagen (z.B. zur Anomalieerkennung).
Sie können die Ergebnisse statistischer Analysen verzerren und die Modellierung erschweren. Daher ist es wichtig, Ausreißer zu identifizieren und den richtigen Umgang mit ihnen zu wählen.
Der erste Ansatz ist die Wertebereiche der Daten zu prüfen. Hier kann man deskriptive Methoden benutzen, um eventuelle verdächtige Werte zu erkennen. Bei numerischen Werten ist der offensichtlichste Ausgangspunkt, den Wertebereich zu überprüfen. Zum Beispiel - was ist der kleinste und größte Wert in unserem Wetter Datensatz:
Prüfen wir zum Beispiel die Mittlere Tagestemperatur (TMK):
wetter.TMK.min(), wetter.TMK.max()
(-14.8, 27.8)
Die Werte liegen durchaus im realistischen Bereich und erfordern keine Änderung notwendig ist. Schauen wir auf die relative Luftfeuchtigkeit (UPM):
wetter.UPM.min(), wetter.UPM.max()
(42.0, 1000.0)
Dann stellen wir fest, dass diese zwischen 42% und 1000% liegt. Letzteres ist nicht möglich und könnte ein Tippfehler sein. Bei solchen fehlerhaften Werten wissen wir allerdings nicht, was der originale Wert war, deshalb ist es sinnvoll ihn mit pd.NA ersetzen. Hierfür können wir die Funktion mask nutzen:
wetter["UPM"]=wetter.UPM.mask(cond=wetter.UPM > 100, other=pd.NA)
Wenn wir jetzt die Min und Max bestimmen, sehen wir, dass die Werte sich jetzt im Definitionsbereich liegen:
wetter.UPM.min(), wetter.UPM.max()
(42.0, 100.0)
Wie wir mit Ausreißern und Anomalien umgehen, werden wir später behandeln.
Fehlende Werte Ersetzen¶
Manchmal möchten man fehlenden Werte durch neuen Wert ersetzen. Hier unterscheidet man unterschiedliche Fälle:
Fehlende Werte mit sinnvollen Standartwerten: Es gibt Datensätze, wo man durchaus sinnvolle Standartwerte annehmen kann für fehlende Werte. Zum Beispiel, zählen wir die Unfälle auf Baustellen pro Tag. Da diese nur registriert werden, wenn welche auftreten, ist für die anderen Tage anzunehmen (aber nicht garantiert), dass keine aufgetreten sind.
Man könnte zum Beispiel annehmen, dass die Schneetiefe in unserem Wetterdatensatz 0 ist (Das wäre allerdings falsch), wenn sie nicht angegeben ist. In diesem Fall können wir die fehlenden Werte
pd.NAmitfillnaersetzen:
wetter.SHK_TAG.fillna(value=0)
0 0.0
1 0.0
2 0.0
3 0.0
4 0.0
...
7204 0.0
7205 0.0
7206 0.0
7207 0.0
7208 0.0
Name: SHK_TAG, Length: 7209, dtype: float64
Wenige Fehlende Werte Ersetzen¶
Bei Zeitreihen, wie den Wetterdaten, kann man fehlende Werte zwischendurch ersetzen, wenn man davon ausgehen kann, dass sie sich nicht schnell ändern. Dazu nutzt man Methoden der Interpolation. Pandas unterstützt
ffill- Ersetzt NA/NaN-Werte, indem Sie die letzte gültige Beobachtung verwenden, um die Lücke zu füllen.bfill- Ersetzt NA/NaN-Werte, indem Sie die nächste gültige Beobachtung nutzt, um die Lücke zu füllen.interpolate- Ersetzt NA/NaN-Werte mit einer Interpolationsmethode, die mit dem Parametermethodangegeben wird:linear- Interpoliert linear zwischen dem letzten und dem nächsten Wert.nearest- Wählt entweder den letzten und dem nächsten Wert, je nachdem welcher zeitlich näher liegt.polynomial- Interpoliert zwischen dem letzten und dem nächsten Wert mit einem Polynom der agebenen Ordnung (z.B.order=5).cubic- Interpoliert zwischen dem letzten und dem nächsten Wert mit einem cubischen Polynom (das Überschwingen vermeidet).
Bei allen diesen Methoden ist empfohlen den Parameter limit zu nutzen. Er bestimmt wie viele nacheinander folgende Werte ersetzt werden dürfen (andere bleiben NA). So mag es akzeptabel sein, ein einzelner Tag zu interpolieren, allerdings nicht eine ganze Woche, da der anzunehmende Interpolationsfehler zu groß wird.
Schauen wir uns die mittlere Temperatur an:
wetter.TMK[:10]
0 -2.1 1 -4.8 2 -12.9 3 -12.9 4 -9.9 5 -9.1 6 -10.8 7 -9.3 8 -1.1 9 2.6 Name: TMK, dtype: float64
Hier fehlen mehrere Werte. Wir können diese interpolieren mit:
wetter["TMK"]=wetter.TMK.interpolate(method="cubic", limit=1)
wetter.TMK[:10]
0 -2.1 1 -4.8 2 -12.9 3 -12.9 4 -9.9 5 -9.1 6 -10.8 7 -9.3 8 -1.1 9 2.6 Name: TMK, dtype: float64
Fehlende Werte Am Anfang und Ende¶
Fehlende Werte am Anfang oder Ende einer Zeitreihe kann diese nicht Interpolieren, da Information über Vorgängerwerte oder Nachfolgerwerte fehlen. In solchen Fällen spricht man von Extrapolation. Prinzipiell kann man hier die Funktionen ffill und bfill verwenden. Da halt allerdings Randwertinformationen fehlen ist der anzunehmende Extrapolationsfehler meist groß, weshalb unbedingt limit zu verwenden ist.
wetter["RSK"]=wetter.RSK.ffill(limit=1)
Fehlende Datumswerte hinzufügen¶
Gerade bei der Analyse von Zeitreihen ist es oft wichtig das Messungen in festem Abstand (Equidistant) aufgenommen werden. Um das zu prüfen müssen wir als erstes die Datumsangabe in unserm Wetterdatensatz in einen nutzbaren Datentyp für Zeiten umwandeln. Dies können wir mit der Funktion pd.to_datetime umwandeln. Dafür müssen wir die originale Datumsspalte MESS_DATUM in einen String umwandeln, der von to_datetime verwendet werden kann und ein String der das format repräsentiert (siehe Umgang mit Zeitstempeln):
wetter["DATUM_DT"] = pd.to_datetime(wetter.MESS_DATUM.astype(str), format="%Y%m%d", utc=True)
Als nächstes empfiehlt es sich den Datensatz nach der Zeit zu sortieren:
wetter.sort_values(by="DATUM_DT", inplace=True) # Sortier nach der Spalte "MESS_DATUM" und ersetzt den Dataframe direkt (inplace)
Dann können wir prüfen, mit welcher Häufigkeit, welche zeitlichen Differenzen auftreten. Wir können dafür die diff Funktion nutzen, um die Zeitdifferenz zu bestimmen. Diese verketten wir mit value_counts. um die Häufigkeit der Differenzen zu berechnen.
wetter.DATUM_DT.diff().value_counts()
DATUM_DT 1 days 7205 2 days 2 3 days 1 Name: count, dtype: int64
Wir sehen, dass in unserem Datensatz mehre Messwerte fehlen, da Differenz von mehr als 1 Tag vorkommen.
Um diese Daten wiederherzustellen können wir die Funktion resample benutzen. Dafür müssen wir zuerst die Datumsspalte zum Index des Dataframes machen, so dass eine richtige mehrdimensionale Zeitreihe draus wird.
wetter.set_index("DATUM_DT", inplace=True)
Jetzt können wir mit resample den Dataframe in eine regelmäßige tägliche Auflösung bringen. Dabei müssen wir eine Funktion zur Interpolation der fehlenden Werte mit angeben.
wetter1D=wetter.resample('1d').ffill(limit=1)
Nun können wir den Index wieder zu eine Spalte machen
wetter1D.reset_index(inplace=True)
Der neue Dataframe enthält jetzt keine fehlenden Werte
wetter1D.DATUM_DT.diff().value_counts()
DATUM_DT 1 days 7212 Name: count, dtype: int64
Fehlende Werte und mathematische Operationen¶
Die Methoden .sum und .mean von Pandas ignorieren fehlende Werte. Berechnen wir den Mittelwert der täglich Sonnenscheindauer (SDK):
wetter1D.SDK.mean()
4.904363699582754
Sie liegt bei 4.9 Studen.
Wenn wir jedoch den Mittelwert entsprechend der Formel für den arithmetischen Mittelwert
$$ \bar{x} = \frac{1}{N} \sum_{i=1}^{N} x_i. $$
selbst berechnen
wetter1D.SDK.sum()/len(wetter1D.SDK)
3.9109801746845974
Dann ergibt sich ein komplett anderes Ergebnis. Dies liegt daran, dass len fehlende Werte nicht ignoriert und daher die Summe durch die Gesamtzahl der Fälle teilen, inklusive der fehlenden Fälle.
In dem Fall wäre die Berechnung mit count richtig, da dann NA Werte ignoriert werden.
wetter1D.SDK.sum()/wetter1D.SDK.count()
4.904363699582754
Wenn wir jedoch einen fehlenden Wert mit einer Zahl vergleichen, ergibt sich False und nicht ein fehlender Wert pd.NA, was formal richtig wäre, da für die fehlenden Werte ja keine Aussage getroffen werden kann. Das kann sehr schnell zu falschen Ergebnissen führen. Wollen wir zum Beispiel die Anzahl der Sonnentage mit mehr als 8 Stunden Sonnenschein bestimmen, so ist es intuitiv zu berechnen:
sonnentage = wetter1D.SDK < 8
sonnentage.value_counts(dropna=False)
SDK True 4180 False 3033 Name: count, dtype: int64
Das ist allerdings Falsch. Wir haben die Informationen über die fehlenden Werte im Prozess verloren und Tage mit fehlenden Werten automatisch zu keinem Sonnentag gemacht. Die richtige Berechnung kann man mit der Funktion map bestimmen, da mit dem Parameter na_action='ignore' enthaltene NA Werte belassen werden:
sonnentage = wetter1D.SDK.map(lambda x: x < 8, na_action='ignore')
sonnentage.value_counts(dropna=False)
SDK True 4180 False 1572 NaN 1461 Name: count, dtype: int64
Dies unterstreicht die Bedeutung der Behandlung von fehlenden Werten in Daten und das man sich mit dem Umgang der Standardfunktionalität von Pandas mit NA vertraut machen sollte.
Konvertierung von Variablen¶
Konvertierung von kategorischen Variablen¶
(convert-categorical-variables-using-pdcut)=
Verwenden von pd.cut¶
pd.cut ist eine dedizierte Funktion von Pandas, um kontinuierliche numerische Daten in vordefinierte Intervalle zu schneiden. Es wird wie folgt aufgerufen:
pd.cut(x, bins, right=True, labels=None)
wo x die Variable ist, die geschnitten werden soll, bins sind die Intervallgrenzen, labels sind die Intervallnamen und right gibt an, ob der rechte Grenzwert im Intervall enthalten ist (right = True bedeutet, dass die Grenzen rechts offen sind). Es ist hauptsächlich für das Aufteilen von kontinuierlichen Werten gedacht, kann aber auch leicht für diskrete Werte verwendet werden. Lassen Sie uns diese Daten in gewünschte Intervalle aufteilen:
wetter1D["TemperaturKlasse"]=pd.cut(wetter1D.TMK,
bins = [-np.inf, 13, 18, 24, 30, np.inf],
labels = ["Cold", "Cool", "Mild", "Warm", "Hot"],
right=False)
wetter1D["TemperaturKlasse"].value_counts(dropna=False)
TemperaturKlasse Cold 4861 Cool 1836 Mild 503 Warm 12 NaN 1 Hot 0 Name: count, dtype: int64
Verwendung von np.where¶
Eine weitere Option ist die Verwendung von np.where, einer vektorisierten Version einer if-else-Anweisung. np.where nimmt drei Argumente entgegen: eine vektorisierte logische Bedingung, den Wert, wenn die Bedingung wahr ist, und den Wert, wenn sie falsch ist. Wir können die Funktion verschachteln, um alternative Bedingungen zu prüfen. Zum Beispiel wollen wir die Heizgradtage bestimmen (Mittlere Temperatur < 15°C) und die Kühlgradtage (Mittlere Temperatur > 22°C).
wetter1D["HeizKuehlTage"] = np.where(wetter1D.TMK > 22, "Kühlgradtag", np.where(wetter1D.TMK < 15, "Heizgradtag", "Normaltag"))
wetter1D["HeizKuehlTage"].value_counts(dropna=False)
HeizKuehlTage Heizgradtag 5611 Normaltag 1559 Kühlgradtag 43 Name: count, dtype: int64
Es ist zu beachten, dass die logische Bedingung in np.where wieder NA Werte auf False mapt. Deshalb sollte man das wieder gezielt behandeln:
wetter1D["HeizKuehlTage"] = np.where(wetter1D.TMK.isna(), pd.NA, np.where(wetter1D.TMK > 22, "Kühlgradtag", np.where(wetter1D.TMK < 15, "Heizgradtag", "Normaltag")))
wetter1D["HeizKuehlTage"].value_counts(dropna=False)
HeizKuehlTage Heizgradtag 5611 Normaltag 1558 Kühlgradtag 43 <NA> 1 Name: count, dtype: int64
Mit der map Funktion lässt sich das auch realisieren:
wetter1D["HeizKuehlTage"] = wetter1D.TMK.map(lambda x: "Heizgradtag" if x < 15 else "Kühlgradtag" if x > 22 else "Normaltag", na_action='ignore')
Ersetzen ausgewählter Werte im Dataframe¶
Häufig ist es notwendig bestimmte Werte gezielt zu ersetzen, auf Basis einer logischen Bedingung zu modifizieren. Dies kann man indem man den .loc-Index eines Dataframes nutzt. Das kann man auch nutzen, um neue Spalten zu berechnen. Wir erstellen eine neue leere Spalte und passen sie anschließend nach unseren Bedürfnissen an. Beachten Sie, dass dies einen gemischten Indexierungsansatz erfordert. Wir werden die Zeilen anhand eines logischen Vektors (logische Bedingung) und die Spalten anhand ihres Namens indizieren. Die Spalte QN_3 im Datensatz zum Beispiel codiert die Datenqualität, mit den folgenden kategorischen Werten.
wetter1D["QNS_4"] = pd.NA
wetter1D.loc[wetter1D.QN_4 == 1, "QNS_4"] = "nur formale Prüfung"
wetter1D.loc[wetter1D.QN_4 == 2, "QNS_4"] = "nach individuellen Kriterien geprüft"
wetter1D.loc[wetter1D.QN_4 == 3, "QNS_4"] = "automatische Prüfung und Korrektur"
wetter1D.loc[wetter1D.QN_4 == 5, "QNS_4"] = "historische, subjektive Verfahren"
wetter1D.loc[wetter1D.QN_4 == 7, "QNS_4"] = "geprüft, gepflegt, nicht korrigiert"
wetter1D.loc[wetter1D.QN_4 == 8, "QNS_4"] = "Qualitätsicherung ausserhalb ROUTINE"
wetter1D.loc[wetter1D.QN_4 == 9, "QNS_4"] = "nicht alle Parameter korrigiert"
wetter1D.loc[wetter1D.QN_4 == 10, "QNS_4"] = "Qualitätsprüfung und Korrektur beendet"
wetter1D["QNS_4"].value_counts(dropna=False)
QNS_4 historische, subjektive Verfahren 7202 automatische Prüfung und Korrektur 3 nur formale Prüfung 2 nach individuellen Kriterien geprüft 2 Qualitätsicherung ausserhalb ROUTINE 2 <NA> 1 nicht alle Parameter korrigiert 1 Name: count, dtype: int64
Für solche komplexeren Mappings kann man auch die map Funktion verwenden und in dieser eine speziell definierte Mappingfunktion.
def QN_Mapping(x):
if x == 1: return "nur formale Prüfung"
if x == 2: return "nach individuellen Kriterien geprüft"
if x == 3: return "automatische Prüfung und Korrektur"
if x == 5: return "historische, subjektive Verfahren"
if x == 7: return "geprüft, gepflegt, nicht korrigiert"
if x == 8: return "Qualitätsicherung ausserhalb ROUTINE"
if x == 9: return "nicht alle Parameter korrigiert"
if x == 10: return "Qualitätsprüfung und Korrektur beendet"
return pd.NA
wetter1D["QNS_4"] = wetter1D.QN_4.map(QN_Mapping, na_action='ignore')
Konvertierung kategorischer Variablen in Dummy-Variablen¶
Im vorherigen Abschnitt haben wir uns damit beschäftigt, Variablen in Kategorien umzuwandeln. In vielen Fällen (z.B. beim Einfügen kategorischer Variablen in statistische Modelle) müssen wir jedoch das Gegenteil tun - Kategorien in Vektoren von Zahlen umwandeln.
QN_Dummies = pd.get_dummies(wetter1D.QNS_4, prefix="QN")
QN_Dummies
| QN_Qualitätsicherung ausserhalb ROUTINE | QN_automatische Prüfung und Korrektur | QN_historische, subjektive Verfahren | QN_nach individuellen Kriterien geprüft | QN_nicht alle Parameter korrigiert | QN_nur formale Prüfung | |
|---|---|---|---|---|---|---|
| 0 | False | False | True | False | False | False |
| 1 | False | False | True | False | False | False |
| 2 | False | True | False | False | False | False |
| 3 | False | True | False | False | False | False |
| 4 | False | False | True | False | False | False |
| ... | ... | ... | ... | ... | ... | ... |
| 7208 | False | False | True | False | False | False |
| 7209 | False | False | True | False | False | False |
| 7210 | False | False | True | False | False | False |
| 7211 | False | False | True | False | False | False |
| 7212 | False | False | True | False | False | False |
7213 rows × 6 columns
Um Kategorien in numerische Werte umzuwandeln gibt es die Funktion pd.factorize. Hier wird eine numerische Serie erstellt der die Kategorien als Index angehängt werden, ähnlich der originalen numerischen Kodierung.
QN_Factors_Values, QN_Factors_Mapping = pd.factorize(wetter1D.QNS_4)
QN_Factors_Values, QN_Factors_Mapping
(array([0, 0, 1, ..., 0, 0, 0]),
Index(['historische, subjektive Verfahren',
'automatische Prüfung und Korrektur', 'nur formale Prüfung',
'nach individuellen Kriterien geprüft',
'Qualitätsicherung ausserhalb ROUTINE',
'nicht alle Parameter korrigiert'],
dtype='object'))
Zu beachten ist, dass die Funktion ein Tupel mit den numerischen Werten und dem Mapping zurück gibt. Wir können die Werte als neue Spalte dem Dataframe hinzufügen
wetter1D["QNF_4"] = QN_Factors_Values
Kombinieren von Daten in Dataframes¶
Verknüpfen von Daten mit pd.concat¶
pd.concat kann Serien und Dataframes auf verschiedene Weise kombinieren. Lassen Sie uns dies anhand einiger Beispiele demonstrieren.
So wollen wir zum Beispiel unseren originalen Wetter Dataframe, um die erstellten Spalten im QN_Dummies erweitern.
wetter_ext = pd.concat((wetter1D, QN_Dummies), axis=1)
wetter_ext
| DATUM_DT | STATIONS_ID | MESS_DATUM | QN_3 | FX | FM | QN_4 | RSK | RSKF | SDK | ... | TemperaturKlasse | HeizKuehlTage | QNS_4 | QNF_4 | QN_Qualitätsicherung ausserhalb ROUTINE | QN_automatische Prüfung und Korrektur | QN_historische, subjektive Verfahren | QN_nach individuellen Kriterien geprüft | QN_nicht alle Parameter korrigiert | QN_nur formale Prüfung | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1947-01-01 00:00:00+00:00 | 4271.0 | 19470101.0 | NaN | NaN | NaN | 5.0 | NaN | NaN | NaN | ... | Cold | Heizgradtag | historische, subjektive Verfahren | 0 | False | False | True | False | False | False |
| 1 | 1947-01-02 00:00:00+00:00 | 4271.0 | 19470101.0 | NaN | NaN | NaN | 5.0 | NaN | NaN | NaN | ... | Cold | Heizgradtag | historische, subjektive Verfahren | 0 | False | False | True | False | False | False |
| 2 | 1947-01-03 00:00:00+00:00 | 4271.0 | 19470103.0 | NaN | NaN | NaN | 3.0 | NaN | NaN | NaN | ... | Cold | Heizgradtag | automatische Prüfung und Korrektur | 1 | False | True | False | False | False | False |
| 3 | 1947-01-04 00:00:00+00:00 | 4271.0 | 19470103.0 | NaN | NaN | NaN | 3.0 | NaN | NaN | NaN | ... | Cold | Heizgradtag | automatische Prüfung und Korrektur | 1 | False | True | False | False | False | False |
| 4 | 1947-01-05 00:00:00+00:00 | 4271.0 | 19470105.0 | NaN | NaN | NaN | 5.0 | NaN | NaN | NaN | ... | Cold | Heizgradtag | historische, subjektive Verfahren | 0 | False | False | True | False | False | False |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 7208 | 1966-09-26 00:00:00+00:00 | 4271.0 | 19660926.0 | 5.0 | NaN | 6.6 | 5.0 | 0.3 | 1.0 | 2.2 | ... | Cool | Heizgradtag | historische, subjektive Verfahren | 0 | False | False | True | False | False | False |
| 7209 | 1966-09-27 00:00:00+00:00 | 4271.0 | 19660927.0 | 5.0 | NaN | 10.0 | 5.0 | 0.0 | 1.0 | 6.1 | ... | Cold | Heizgradtag | historische, subjektive Verfahren | 0 | False | False | True | False | False | False |
| 7210 | 1966-09-28 00:00:00+00:00 | 4271.0 | 19660928.0 | 5.0 | NaN | 4.5 | 5.0 | 0.0 | 0.0 | 9.9 | ... | Cold | Heizgradtag | historische, subjektive Verfahren | 0 | False | False | True | False | False | False |
| 7211 | 1966-09-29 00:00:00+00:00 | 4271.0 | 19660929.0 | 5.0 | NaN | 3.3 | 5.0 | 0.0 | 0.0 | 7.8 | ... | Cold | Heizgradtag | historische, subjektive Verfahren | 0 | False | False | True | False | False | False |
| 7212 | 1966-09-30 00:00:00+00:00 | 4271.0 | 19660930.0 | 5.0 | NaN | 3.5 | 5.0 | 0.0 | 0.0 | 7.8 | ... | Cold | Heizgradtag | historische, subjektive Verfahren | 0 | False | False | True | False | False | False |
7213 rows × 30 columns
Dieses Beispiel zeigt die wichtigsten Argumente von pd.concat. Das erste Argument ist ein beliebig langes Tuple von Daten (Serien oder Dataframes), die wir zusammenführen möchten (alternativ kann auch eine Liste verwendet werden). Wir setzen den Parameter axis=1, um anzugeben, dass wir die Serien spaltenweise zusammenführen möchten, nicht zeilenweise.
Wenn die Dataframes kompatibel sind, können wir sie auch zeilenweise kombinieren, indem wir axis=0 angeben.
Zum Beispiel wollen wir unseren Wetterdatensatz um die Werte nach 1960 erweitern.
wetter_ab_1960 = pd.read_csv("../data/Wetter/warnemuende_ab_1960.csv", sep=';', na_values=['-999','NA'])
wetter_ab_1960["DATUM_DT"] = pd.to_datetime(wetter_ab_1960.MESS_DATUM.astype(str), format="%Y%m%d")
wetter_ab_1960
| STATIONS_ID | MESS_DATUM | QN_3 | FX | FM | QN_4 | RSK | RSKF | SDK | SHK_TAG | NM | VPM | PM | TMK | UPM | TXK | TNK | TGK | eor | DATUM_DT | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 4271 | 19600101 | 5.0 | NaN | 4.1 | 5 | 1.4 | 1.0 | 0.000 | 0.0 | 7.8 | 8.9 | 1003.40 | 7.0 | 90.00 | 7.9 | 4.9 | 4.1 | eor | 1960-01-01 |
| 1 | 4271 | 19600102 | 5.0 | NaN | 2.4 | 5 | 1.4 | 1.0 | 0.000 | 0.0 | 8.0 | 9.7 | 1004.80 | 6.8 | 97.00 | 8.0 | 6.3 | 5.2 | eor | 1960-01-02 |
| 2 | 4271 | 19600103 | 5.0 | NaN | 1.7 | 5 | 0.1 | 1.0 | 0.000 | 0.0 | 7.8 | 8.8 | 1014.20 | 5.2 | 99.00 | 6.7 | 4.8 | 4.0 | eor | 1960-01-03 |
| 3 | 4271 | 19600104 | 5.0 | NaN | 2.5 | 5 | 0.0 | 1.0 | 0.000 | 0.0 | 8.0 | 8.3 | 1027.10 | 4.3 | 98.00 | 5.3 | 3.3 | 3.4 | eor | 1960-01-04 |
| 4 | 4271 | 19600105 | 5.0 | NaN | 7.1 | 5 | 1.6 | 1.0 | 0.000 | 0.0 | 7.8 | 9.1 | 1016.00 | 5.9 | 95.00 | 9.3 | 3.8 | 3.5 | eor | 1960-01-05 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 23439 | 4271 | 20240304 | 1.0 | 11.0 | 3.1 | 1 | 0.0 | 0.0 | 8.667 | 0.0 | 3.9 | 8.3 | 1010.80 | 7.1 | 81.54 | 12.0 | 3.1 | 1.8 | eor | 2024-03-04 |
| 23440 | 4271 | 20240305 | 1.0 | 10.2 | 3.5 | 1 | 0.0 | 6.0 | 1.183 | 0.0 | 5.7 | 6.6 | 1017.63 | 3.7 | 82.50 | 6.0 | 2.1 | 0.7 | eor | 2024-03-05 |
| 23441 | 4271 | 20240306 | 1.0 | 8.1 | 2.7 | 1 | 0.0 | 0.0 | 1.383 | 0.0 | 7.7 | 7.1 | 1024.36 | 4.2 | 85.96 | 6.2 | 2.8 | 2.4 | eor | 2024-03-06 |
| 23442 | 4271 | 20240307 | 1.0 | 7.4 | 2.7 | 1 | 0.0 | 0.0 | 7.783 | 0.0 | 3.1 | 6.1 | 1026.72 | 4.4 | 74.04 | 9.5 | 0.6 | -1.1 | eor | 2024-03-07 |
| 23443 | 4271 | 20240308 | 1.0 | 8.2 | 2.7 | 1 | 0.0 | 0.0 | 5.667 | 0.0 | 2.8 | 6.1 | 1020.17 | 2.5 | 84.29 | 8.9 | -0.4 | -3.1 | eor | 2024-03-08 |
23444 rows × 20 columns
Es ist wichtig zu erkennen, dass beim horizontalen Verketten von Daten pd.concat die Beobachtungen nicht zeilenweise, sondern nach Index kombiniert. Wenn wir beispielsweise versuchen beide Dataframes direkt zu kombinieren so wird das nicht gut ausgehen:
wetter_all=pd.concat((wetter1D, wetter_ab_1960), axis=0)
wetter_all
| DATUM_DT | STATIONS_ID | MESS_DATUM | QN_3 | FX | FM | QN_4 | RSK | RSKF | SDK | ... | TMK | UPM | TXK | TNK | TGK | eor | TemperaturKlasse | HeizKuehlTage | QNS_4 | QNF_4 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1947-01-01 00:00:00+00:00 | 4271.0 | 19470101.0 | NaN | NaN | NaN | 5.0 | NaN | NaN | NaN | ... | -2.1 | 78.00 | -1.5 | -3.3 | -5.8 | eor | Cold | Heizgradtag | historische, subjektive Verfahren | 0.0 |
| 1 | 1947-01-02 00:00:00+00:00 | 4271.0 | 19470101.0 | NaN | NaN | NaN | 5.0 | NaN | NaN | NaN | ... | -2.1 | 78.00 | -1.5 | -3.3 | -5.8 | eor | Cold | Heizgradtag | historische, subjektive Verfahren | 0.0 |
| 2 | 1947-01-03 00:00:00+00:00 | 4271.0 | 19470103.0 | NaN | NaN | NaN | 3.0 | NaN | NaN | NaN | ... | -4.8 | 80.00 | -2.4 | -6.2 | -4.5 | eor | Cold | Heizgradtag | automatische Prüfung und Korrektur | 1.0 |
| 3 | 1947-01-04 00:00:00+00:00 | 4271.0 | 19470103.0 | NaN | NaN | NaN | 3.0 | NaN | NaN | NaN | ... | -4.8 | 80.00 | -2.4 | -6.2 | -4.5 | eor | Cold | Heizgradtag | automatische Prüfung und Korrektur | 1.0 |
| 4 | 1947-01-05 00:00:00+00:00 | 4271.0 | 19470105.0 | NaN | NaN | NaN | 5.0 | NaN | NaN | NaN | ... | -12.9 | 79.00 | -9.4 | -14.0 | -16.0 | eor | Cold | Heizgradtag | historische, subjektive Verfahren | 0.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 23439 | 2024-03-04 00:00:00 | 4271.0 | 20240304.0 | 1.0 | 11.0 | 3.1 | 1.0 | 0.0 | 0.0 | 8.667 | ... | 7.1 | 81.54 | 12.0 | 3.1 | 1.8 | eor | NaN | NaN | NaN | NaN |
| 23440 | 2024-03-05 00:00:00 | 4271.0 | 20240305.0 | 1.0 | 10.2 | 3.5 | 1.0 | 0.0 | 6.0 | 1.183 | ... | 3.7 | 82.50 | 6.0 | 2.1 | 0.7 | eor | NaN | NaN | NaN | NaN |
| 23441 | 2024-03-06 00:00:00 | 4271.0 | 20240306.0 | 1.0 | 8.1 | 2.7 | 1.0 | 0.0 | 0.0 | 1.383 | ... | 4.2 | 85.96 | 6.2 | 2.8 | 2.4 | eor | NaN | NaN | NaN | NaN |
| 23442 | 2024-03-07 00:00:00 | 4271.0 | 20240307.0 | 1.0 | 7.4 | 2.7 | 1.0 | 0.0 | 0.0 | 7.783 | ... | 4.4 | 74.04 | 9.5 | 0.6 | -1.1 | eor | NaN | NaN | NaN | NaN |
| 23443 | 2024-03-08 00:00:00 | 4271.0 | 20240308.0 | 1.0 | 8.2 | 2.7 | 1.0 | 0.0 | 0.0 | 5.667 | ... | 2.5 | 84.29 | 8.9 | -0.4 | -3.1 | eor | NaN | NaN | NaN | NaN |
30657 rows × 24 columns
Obwohl beide Dataframes eine unterschiedliche Anzahl an Spalten haben (Es fehlen bei wetter_ab_1960 die Spalten, die wir hinzugefügt haben), kann concat beide Dataframes kombinieren. Hierbei werden fehlende Spalten mit np.NaN aufgefüllt. Deshalb ist es sinnvoll erst zusammenzufügen, bevor man abgeleitete Werte berechnet. Dies können wir korrigieren, indem wir die fehlenden Werte neu berechnen.
wetter_all["TemperaturKlasse"]=pd.cut(wetter_all.TMK, bins = [-np.inf, 13, 18, 24, 30, np.inf], labels = ["Cold", "Cool", "Mild", "Warm", "Hot"], right=False)
wetter_all["HeizKuehlTage"] = wetter_all.TMK.map(lambda x: "Heizgradtag" if x < 15 else "Kühlgradtag" if x > 22 else "Normaltag", na_action='ignore')
wetter_all["QNS_4"] = wetter_all.QN_4.map(QN_Mapping, na_action='ignore')
wetter_all["QNF_4"], _ = pd.factorize(wetter_all.QNS_4)
Dataframe kombinieren¶
Meist will man nicht nur Daten kombinieren, die nicht gleich groß sind oder den gleichen Index haben. Zum Beispiel wollen wir die Wetterdaten mit den Energiedaten der Universität Rostock kombinieren, um diese später zu analysieren.
uros_egy=pd.read_csv("../data/UROS/Energy1D_kW.csv", parse_dates=["Date"])
uros_egy.head()
| Date | EV_HT_740 | EV_NT_740 | E_AV_Lab | E_SV_Lab | ES_Lab | |
|---|---|---|---|---|---|---|
| 0 | 2020-12-30 00:00:00+00:00 | NaN | NaN | NaN | NaN | NaN |
| 1 | 2020-12-31 00:00:00+00:00 | NaN | NaN | 1256.0 | 291.0 | 5.0 |
| 2 | 2021-01-01 00:00:00+00:00 | 0.0 | 4080.0 | 1221.0 | 290.0 | 1.0 |
| 3 | 2021-01-02 00:00:00+00:00 | 1170.0 | 2630.0 | 1243.0 | 284.0 | 2.0 |
| 4 | 2021-01-03 00:00:00+00:00 | 0.0 | 3750.0 | 1222.0 | 283.0 | 2.0 |
Die Daten können wir mit der Methode pd.merge() kombinieren, die wie ein SQL Join funktioniert. Hierbei können wir die Spalten die gematcht werden sollen mit left_on und right_on spezifizieren (oder on wenn die Spalten gleich sind). Mit how="left" spezifizieren wir, dass nur die Zeilen genommen werden sollen, die im Energiedatensatz vorhanden sind.
uros_egy_weater=pd.merge(uros_egy, wetter_all, right_on="DATUM_DT", left_on="Date", how="left")
uros_egy_weater.head()
--------------------------------------------------------------------------- ValueError Traceback (most recent call last) Cell In[50], line 1 ----> 1 uros_egy_weater=pd.merge(uros_egy, wetter_all, right_on="DATUM_DT", left_on="Date", how="left") 2 uros_egy_weater.head() File /opt/miniconda3/envs/lehre4/lib/python3.12/site-packages/pandas/core/reshape/merge.py:170, in merge(left, right, how, on, left_on, right_on, left_index, right_index, sort, suffixes, copy, indicator, validate) 155 return _cross_merge( 156 left_df, 157 right_df, (...) 167 copy=copy, 168 ) 169 else: --> 170 op = _MergeOperation( 171 left_df, 172 right_df, 173 how=how, 174 on=on, 175 left_on=left_on, 176 right_on=right_on, 177 left_index=left_index, 178 right_index=right_index, 179 sort=sort, 180 suffixes=suffixes, 181 indicator=indicator, 182 validate=validate, 183 ) 184 return op.get_result(copy=copy) File /opt/miniconda3/envs/lehre4/lib/python3.12/site-packages/pandas/core/reshape/merge.py:807, in _MergeOperation.__init__(self, left, right, how, on, left_on, right_on, left_index, right_index, sort, suffixes, indicator, validate) 803 self._validate_tolerance(self.left_join_keys) 805 # validate the merge keys dtypes. We may need to coerce 806 # to avoid incompatible dtypes --> 807 self._maybe_coerce_merge_keys() 809 # If argument passed to validate, 810 # check if columns specified as unique 811 # are in fact unique. 812 if validate is not None: File /opt/miniconda3/envs/lehre4/lib/python3.12/site-packages/pandas/core/reshape/merge.py:1512, in _MergeOperation._maybe_coerce_merge_keys(self) 1510 # datetimelikes must match exactly 1511 elif needs_i8_conversion(lk.dtype) and not needs_i8_conversion(rk.dtype): -> 1512 raise ValueError(msg) 1513 elif not needs_i8_conversion(lk.dtype) and needs_i8_conversion(rk.dtype): 1514 raise ValueError(msg) ValueError: You are trying to merge on datetime64[ns, UTC] and object columns for key 'Date'. If you wish to proceed you should use pd.concat
Hierbei kann es bei Spalten vom Typ Datetime schnell zu Problemen kommen. Was daran liegt, dass es bei dem Datentypen schnell zu inkompabilitäten gibt, die ggf. nicht direkt ersichtlich sind. Wenn das auftritt hilft es meist, beide Spalten nochmal neu zu konvertieren.
uros_egy["Date"]=pd.to_datetime(uros_egy['Date'], utc=True)
wetter_all["DATUM_DT"]=pd.to_datetime(wetter_all['DATUM_DT'], utc=True)
uros_egy_weater=pd.merge(uros_egy, wetter_all, right_on="DATUM_DT", left_on="Date", how="left")
uros_egy_weater.head()
| Date | EV_HT_740 | EV_NT_740 | E_AV_Lab | E_SV_Lab | ES_Lab | DATUM_DT | STATIONS_ID | MESS_DATUM | QN_3 | ... | TMK | UPM | TXK | TNK | TGK | eor | TemperaturKlasse | HeizKuehlTage | QNS_4 | QNF_4 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2020-12-30 00:00:00+00:00 | NaN | NaN | NaN | NaN | NaN | 2020-12-30 00:00:00+00:00 | 4271.0 | 20201230.0 | 10.0 | ... | 4.0 | 81.0 | 4.6 | 2.9 | 2.2 | eor | Cold | Heizgradtag | nicht alle Parameter korrigiert | 5 |
| 1 | 2020-12-31 00:00:00+00:00 | NaN | NaN | 1256.0 | 291.0 | 5.0 | 2020-12-31 00:00:00+00:00 | 4271.0 | 20201231.0 | 10.0 | ... | 3.4 | 83.0 | 4.4 | 2.3 | 0.9 | eor | Cold | Heizgradtag | nicht alle Parameter korrigiert | 5 |
| 2 | 2021-01-01 00:00:00+00:00 | 0.0 | 4080.0 | 1221.0 | 290.0 | 1.0 | 2021-01-01 00:00:00+00:00 | 4271.0 | 20210101.0 | 10.0 | ... | 2.0 | 90.0 | 3.0 | 1.1 | 0.3 | eor | Cold | Heizgradtag | nicht alle Parameter korrigiert | 5 |
| 3 | 2021-01-02 00:00:00+00:00 | 1170.0 | 2630.0 | 1243.0 | 284.0 | 2.0 | 2021-01-02 00:00:00+00:00 | 4271.0 | 20210102.0 | 10.0 | ... | 3.3 | 95.0 | 4.0 | 2.6 | 2.0 | eor | Cold | Heizgradtag | nicht alle Parameter korrigiert | 5 |
| 4 | 2021-01-03 00:00:00+00:00 | 0.0 | 3750.0 | 1222.0 | 283.0 | 2.0 | 2021-01-03 00:00:00+00:00 | 4271.0 | 20210103.0 | 10.0 | ... | 3.5 | 81.0 | 4.6 | 2.4 | 0.8 | eor | Cold | Heizgradtag | nicht alle Parameter korrigiert | 5 |
5 rows × 30 columns
Duplikate entfernen¶
Nachdem wir beide Datensätze zusammengefügt haben, ergibt sich das neue Problem, duplizierter Daten. Das kann in Datensätzen vorkommen, so dass es immer sinnvoll ist, auf Duplikate zu prüfen. Hierfür gibt es die Funktion duplicated. Sie gibt einen boolesche Serie zurück, die Wahr ist für Zeilen, wo alle Werte doppelt vorkommen.
sum(wetter_all.duplicated())
2465
Das ist nur sinvoll, wenn sich Zeilen vollständig wiederholen. In unserm Fall ist das Datum, der eigentliche Index und es ist empfohlen duplicated auf diesen anzuwenden. Wenn wir unseren zusammengefügte Dataframe prüfen, so sehen wir, dass wir einige Duplikate haben, d.h. Daten für die mehr als eine Messung existiert.
sum(wetter_all.duplicated(subset=['DATUM_DT']))
2465
Um diese herauszufiltern können wir die Funktion drop_duplicates nutzen, die ähnliche Parameter verwendet.
wetter_all.drop_duplicates(subset=['DATUM_DT'], inplace=True)
wetter_all.shape
(28192, 24)
Damit haben wir jetzt einen gereinigten Dataframe, den wir uns für die weitere Verwendung abspeichern.
wetter_all.to_csv("../data/Wetter/warnemuende_clean.csv", sep=';', index=False)
uros_egy_weater.to_csv("../data/UROS/Energy1D_weather_clean.csv", index=False)
Dataframes Transformieren¶
Bisher haben wir mit einem Datensatz in Spaltendarstellung gearbeitet. Das ist für uns Menschen eine gewohnte tabellarische Darstellung. Für viele Berechnungen und Visualisierungen, ist das allerdings nicht immer das beste Format. Da braucht man häufig die Daten in einer Zeilendarstellung.
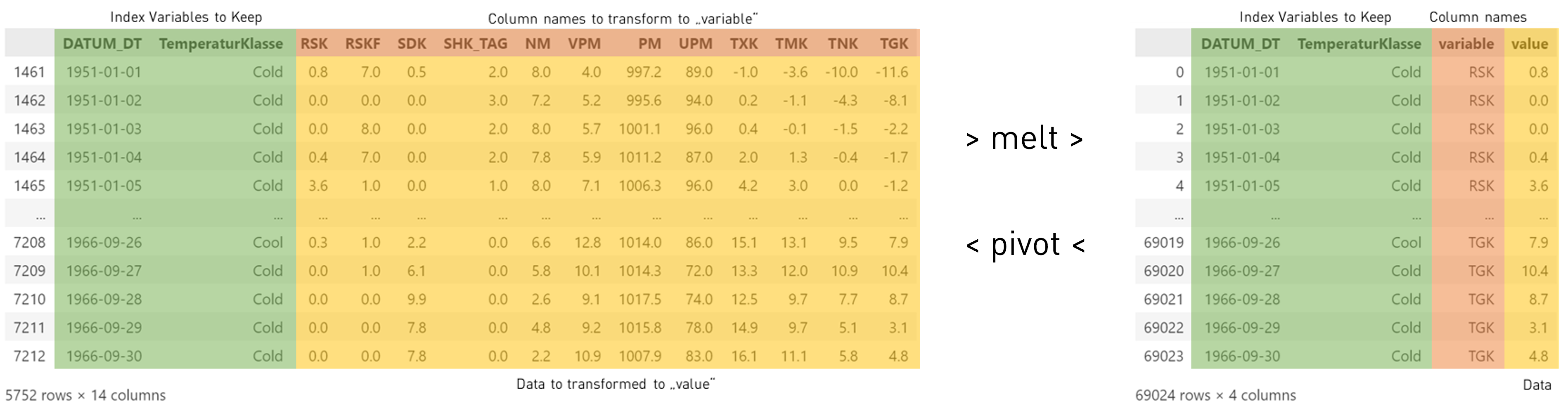
wetter_melted = wetter_all.melt(id_vars=['DATUM_DT', "TemperaturKlasse"], value_vars=["TXK","TMK","TNK"])
wetter_melted
| DATUM_DT | TemperaturKlasse | variable | value | |
|---|---|---|---|---|
| 0 | 1947-01-01 00:00:00+00:00 | Cold | TXK | -1.5 |
| 1 | 1947-01-02 00:00:00+00:00 | Cold | TXK | -1.5 |
| 2 | 1947-01-03 00:00:00+00:00 | Cold | TXK | -2.4 |
| 3 | 1947-01-04 00:00:00+00:00 | Cold | TXK | -2.4 |
| 4 | 1947-01-05 00:00:00+00:00 | Cold | TXK | -9.4 |
| ... | ... | ... | ... | ... |
| 84571 | 2024-03-04 00:00:00+00:00 | Cold | TNK | 3.1 |
| 84572 | 2024-03-05 00:00:00+00:00 | Cold | TNK | 2.1 |
| 84573 | 2024-03-06 00:00:00+00:00 | Cold | TNK | 2.8 |
| 84574 | 2024-03-07 00:00:00+00:00 | Cold | TNK | 0.6 |
| 84575 | 2024-03-08 00:00:00+00:00 | Cold | TNK | -0.4 |
84576 rows × 4 columns
Aus der Zeilendarstellung könnten wir jetzt ein einzelnes ML-Modell bauen, was den Zusammenhang zwischen der Temperaturklasse und den Werten in value lernt und variable nur als Unterscheidungskriterium nutzt. Alternativ können wir damit auch die Zeitreihen einfacher darstellen. So lässt sich damit ein sehr übersichtliches Diagramm zum Vergleich aller Zeitreihen erstellen. Im nächsten Abschnitt Visuelle Datenanalyse gehen wir detaillierte darauf ein.
import plotly.express as px
px.line(wetter_melted, x="DATUM_DT", y="value", facet_row ="variable")
Diese Zeilendarstellung wird auch oft bei komplexen Dataframes mit vielen kategorischen Variablen benutzt. So gibt es viele Datensätze des Statistischen Bundesamtes auf dem GENESIS-Portal im CSV-Flat format, was deutlich einfacher zu verarbeiten ist. Allerdings muss dann der Datensatz aus der Reihendarstellung in eine Spaltendarstellung überführt werden.
Hierfür bietet Pandas die Methode pivot an. Jeder, der sich gewundert hat, wofür man die Pivot-Darstellung in Excel nutzt, hat jetzt eine Antwort. Ähnlich zur melt-Methode, müssen wir bei der pivot-Methode die Spalten identifizieren, welche die Werte values enthält, die Spalte(n) columns welche in neue Spaltennamen umzuwandeln sind und die beizubehaltenden Indexe index.
wetter_hardened = wetter_melted.pivot(columns='variable', index=['DATUM_DT', "TemperaturKlasse"], values='value')
wetter_hardened
| variable | TMK | TNK | TXK | |
|---|---|---|---|---|
| DATUM_DT | TemperaturKlasse | |||
| 1947-01-01 00:00:00+00:00 | Cold | -2.1 | -3.3 | -1.5 |
| 1947-01-02 00:00:00+00:00 | Cold | -2.1 | -3.3 | -1.5 |
| 1947-01-03 00:00:00+00:00 | Cold | -4.8 | -6.2 | -2.4 |
| 1947-01-04 00:00:00+00:00 | Cold | -4.8 | -6.2 | -2.4 |
| 1947-01-05 00:00:00+00:00 | Cold | -12.9 | -14.0 | -9.4 |
| ... | ... | ... | ... | ... |
| 2024-03-04 00:00:00+00:00 | Cold | 7.1 | 3.1 | 12.0 |
| 2024-03-05 00:00:00+00:00 | Cold | 3.7 | 2.1 | 6.0 |
| 2024-03-06 00:00:00+00:00 | Cold | 4.2 | 2.8 | 6.2 |
| 2024-03-07 00:00:00+00:00 | Cold | 4.4 | 0.6 | 9.5 |
| 2024-03-08 00:00:00+00:00 | Cold | 2.5 | -0.4 | 8.9 |
28192 rows × 3 columns
Mit der bekannten Methode reset_index() wandeln wir den Index in Spalten um:
wetter_hardened.reset_index()
| variable | DATUM_DT | TemperaturKlasse | TMK | TNK | TXK |
|---|---|---|---|---|---|
| 0 | 1947-01-01 00:00:00+00:00 | Cold | -2.1 | -3.3 | -1.5 |
| 1 | 1947-01-02 00:00:00+00:00 | Cold | -2.1 | -3.3 | -1.5 |
| 2 | 1947-01-03 00:00:00+00:00 | Cold | -4.8 | -6.2 | -2.4 |
| 3 | 1947-01-04 00:00:00+00:00 | Cold | -4.8 | -6.2 | -2.4 |
| 4 | 1947-01-05 00:00:00+00:00 | Cold | -12.9 | -14.0 | -9.4 |
| ... | ... | ... | ... | ... | ... |
| 28187 | 2024-03-04 00:00:00+00:00 | Cold | 7.1 | 3.1 | 12.0 |
| 28188 | 2024-03-05 00:00:00+00:00 | Cold | 3.7 | 2.1 | 6.0 |
| 28189 | 2024-03-06 00:00:00+00:00 | Cold | 4.2 | 2.8 | 6.2 |
| 28190 | 2024-03-07 00:00:00+00:00 | Cold | 4.4 | 0.6 | 9.5 |
| 28191 | 2024-03-08 00:00:00+00:00 | Cold | 2.5 | -0.4 | 8.9 |
28192 rows × 5 columns
und datenbanken