Machine
Learning

Joern Ploennigs

Dimensionsreduktion

Methoden zur Dimensionsreduktion werden im Machine Learning immer dann genutzt, wenn Datensätze vereinfacht werden sollen, um sie besser zu verstehen oder schneller zu erlernen. Hierbei teilt man die Verfahren in zwei Anwendungsfälle:

• Reduktion der Anzahl an Variablen in sehr großen Datensätzen mittels der Hauptkomponentenanalyse
• Reduktion der Anzahl an Beobachtungen, um typische Muster abzuleiten mittels Matrixfaktorisierung

Hauptkomponentenanalyse (PCA)

Methode

Die Hauptkomponentenanalyse (en. Principal Component Analysis, PCA) wird eingesetzt um Datensätze mit vielen Variablen zu vereinfach und dadurch sie besser verstehen zu können als auch um kompaktere Modelle zu trainieren. Das ist insbesondere bei Datensätzen mit vielen, stark korrelierten Variablen sinnvoll, da sowohl Nutzer die vielen Variablen nicht verstehen können als auch die Variblen in den ML-Modellen nicht sauber getrennt werden können (zur Erinnerung: viele Modelle nehmen an das die Variblen statistisch unabhängig sind, also nicht korreliert sind).

Wir betrachten den bekannten Energie- und Wetter Datensatz.

import numpy as np # Import von NumPy
import pandas as pd # Import von Pandas
                                
egywth = pd.read_csv("../data/UROS/Energy1D_weather_clean.csv", parse_dates=[0])
egywth.head()

	Date	EV_HT_740	EV_NT_740	E_AV_Lab	E_SV_Lab	ES_Lab	DATUM_DT	STATIONS_ID	MESS_DATUM	QN_3	...	TMK	UPM	TXK	TNK	TGK	eor	TemperaturKlasse	HeizKuehlTage	QNS_4	QNF_4
0	2020-12-30	NaN	NaN	NaN	NaN	NaN	2020-12-30	4271.0	20201230.0	10.0	...	4.0	81.0	4.6	2.9	2.2	eor	Cold	Heizgradtag	nicht alle Parameter korrigiert	5
1	2020-12-31	NaN	NaN	1256.0	291.0	5.0	2020-12-31	4271.0	20201231.0	10.0	...	3.4	83.0	4.4	2.3	0.9	eor	Cold	Heizgradtag	nicht alle Parameter korrigiert	5
2	2021-01-01	0.0	4080.0	1221.0	290.0	1.0	2021-01-01	4271.0	20210101.0	10.0	...	2.0	90.0	3.0	1.1	0.3	eor	Cold	Heizgradtag	nicht alle Parameter korrigiert	5
3	2021-01-02	1170.0	2630.0	1243.0	284.0	2.0	2021-01-02	4271.0	20210102.0	10.0	...	3.3	95.0	4.0	2.6	2.0	eor	Cold	Heizgradtag	nicht alle Parameter korrigiert	5
4	2021-01-03	0.0	3750.0	1222.0	283.0	2.0	2021-01-03	4271.0	20210103.0	10.0	...	3.5	81.0	4.6	2.4	0.8	eor	Cold	Heizgradtag	nicht alle Parameter korrigiert	5

5 rows × 30 columns

Wir analysieren vom Datensatz allerdings nur die numerischen, nicht-NA Spalten, weshalb wir sie selektieren.

egywthNumber = egywth.select_dtypes(include='number').dropna()
egywthNumber = egywthNumber[['EV_HT_740', 'EV_NT_740', 'E_AV_Lab', 'E_SV_Lab', 'ES_Lab', 'FX', 'FM', 'RSK', 'RSKF', 'SDK', 'SHK_TAG', 'NM', 'VPM', 'PM', 'TMK', 'UPM', 'TXK', 'TNK', 'TGK']]

Schritt 1 - Datenzentrierung: Die Daten werden zentriert, indem der Mittelwert jeder Dimension subtrahiert wird. Dadurch sind liegen alle Daten um den Ursprung herum.

$$ \boldsymbol X_\text{cent}​ =\boldsymbol X − \boldsymbol μ_X. $$

egywthCentered = egywthNumber - egywthNumber.mean()
egywthCentered.head()

	EV_HT_740	EV_NT_740	E_AV_Lab	E_SV_Lab	ES_Lab	FX	FM	RSK	RSKF	SDK	SHK_TAG	NM	VPM	PM	TMK	UPM	TXK	TNK	TGK
2	-1245.840611	1258.984716	27.776201	16.925764	-37.293668	-5.778166	-2.222162	1.699017	3.745633	-4.973059	-0.177948	2.145524	-3.410153	-8.547838	-7.610699	12.610622	-9.458843	-5.770197	-4.874891
3	-75.840611	-191.015284	49.776201	10.925764	-36.293668	-5.578166	-3.022162	-0.800983	3.745633	-4.973059	-0.177948	2.145524	-2.510153	-0.947838	-6.310699	17.610622	-8.458843	-4.270197	-3.174891
4	-1245.840611	928.984716	28.776201	9.925764	-36.293668	0.521834	-0.022162	-1.400983	1.745633	-4.973059	-0.177948	2.045524	-3.410153	4.852162	-6.110699	3.610622	-7.858843	-4.470197	-4.374891
5	1994.159389	-1711.015284	69.776201	21.925764	-33.293668	2.521834	2.177838	-1.100983	1.745633	-4.973059	-0.177948	2.045524	-3.110153	5.752162	-6.010699	6.610622	-8.058843	-3.870197	-2.774891
6	2224.159389	-1701.015284	152.776201	25.925764	-37.293668	3.721834	2.377838	1.499017	3.745633	-4.973059	-0.177948	2.145524	-2.810153	5.252162	-5.910699	10.610622	-7.758843	-3.870197	-2.574891

Schritt 2 - Berechnung der Kovarianzmatrix: Die Kovarianzmatrix $C$ wird berechnet, um die Streuung und Korrelation zwischen den verschiedenen Dimensionen zu erfassen.

$$ \boldsymbol C =\frac{\boldsymbol X_\text{cent}^T − \boldsymbol X_\text{cent}}{n-1} . $$

cov_matrix = np.cov(egywthCentered, rowvar=False)

Schritt 3 - Eigenwertzerlegung der Kovarianzmatrix: Die Kovarianzmatrix wird einer Eigenwertzerlegung unterzogen, um die Eigenwerte und Eigenvektoren zu berechnen. Die Eigenvektoren repräsentieren die Richtungen der größten Varianz, und die Eigenwerte repräsentieren die Größe der Varianz in diesen Richtungen. Der Eigenvektor einer quadratischen Matrix ist ein Vektor, der durch die Matrix nur um einen skalaren Faktor, den Eigenwert $λ$, gestreckt oder gestaucht wird. Mathematisch ausgedrückt:

$$ \boldsymbol C \boldsymbol v=\lambda \boldsymbol v $$

dabei ist $\lambda$ der skalare Eigenwert und $\boldsymbol v$ der zugehörige Eigenvektor.

# Berechne die Eigenwerte und Eigenvektoren
eigenvalues, eigenvectors = np.linalg.eig(cov_matrix)

Schritt 4 - Auswahl der Hauptkomponenten: Die Hauptkomponenten (Principal Components) sind die Eigenvektoren, die den größten Eigenwerten entsprechen. Diese Eigenvektoren definieren die neuen Achsen des transformierten Datenraums. Hierfür wählen wir die besten $n$ Komponenten in der Matrix $\boldsymbol W$.

# Sortiere die Eigenvektoren nach absteigenden Eigenwerten
idx = np.argsort(eigenvalues)[::-1]
eigenvalues = eigenvalues[idx]
eigenvectors = eigenvectors[:, idx]

# Wähle die n-Hauptkomponenten
n_components = 2
eigenvalues_sub = eigenvalues[:n_components]
W = eigenvectors[:, :n_components]

Schritt 5 - Transformation der Daten: Die ursprünglichen Daten werden auf die neuen Hauptkomponenten projiziert, um die transformierten Daten zu erhalten.

$$ \boldsymbol X_\text{pca} = \boldsymbol X_\text{cent} \cdot \boldsymbol W $$

# Transformiere die Daten
egywth_pca = np.dot(egywthCentered, W)
egywth_pca

array([[1764.35300097, -144.63239642],
       [ -70.67495979,  177.86671771],
       [1547.04272956,   99.44054371],
       ...,
       [ 920.66526878,  888.17908265],
       [ 914.15695   ,  895.99134945],
       [ 803.76433239, 1030.65117329]])

PCA mit SciKit-Learn

Natürlich gibt es dafür auch eine einfache Implementation in sklearn, die wir wie gewohnt einsetzen. Wir können zum Training fit benutzen. Wollen wir allerdings gleich die Komponenten erhalten bietet sich alternativ fit_transform an:

from sklearn.decomposition import PCA

pcam = PCA(n_components=2)
components = pcam.fit_transform(egywthNumber)

Wir können uns die Eigenwerte am Attribute singular_values_ auslesen. Es heißt singular_values_ weil die Eigenwerte nur für quadratische Matritzen definiert sind.

pcam.singular_values_

array([61197.4192215 , 11416.98508508])

Wir können uns auch mit explained_variance_ratio_ die erklärte Varianz ausgeben lassen.

print(pcam.explained_variance_ratio_)

[0.96270602 0.0335066 ]

Hier sehen wir, dass die erste Komponente mit 96.7% den Großteil der Varianz erklärt, die zweite mit 3% deutlich weniger.

Als nächstes wollen wir die Komponenten visualisieren. Das ist ein weiterer wichtiger Anwendungsbereich von PCA, da sich Datensätze mit sehr vielen Variablen schlecht visualisieren lassen, kann man sie mit PCA auf ein 2D oder 3D Dartstellung reduzieren.

import plotly.express as px
# Visualisierung der transformierten Daten
fig = px.scatter(components, x=0, y=1, width=500, height=500)
fig.update_layout( xaxis_title="Hauptkomponente 1", yaxis_title="Hauptkomponente 2")
# Visualisierung der Eigenvektoren
loadings = pcam.components_.T * np.sqrt(pcam.explained_variance_)
for i, feature in enumerate(egywthCentered.columns):
    fig.add_annotation(ax=0, ay=0, axref="x", ayref="y", x=loadings[i, 0], y=loadings[i, 1], showarrow=True, arrowsize=2, arrowhead=2, xanchor="right", yanchor="top")
    fig.add_annotation( x=loadings[i, 0], y=loadings[i, 1], ax=0, ay=0, xanchor="center", yanchor="bottom", text=feature, yshift=5 )
fig.show()

Was wir in dem Diagram erkennen können ist, dass es drei Cluster um "EV_NT_740", "EV_HT_740", "E_AV_Lab". Um den letzteren gruppieren sich auch die ganzen Wetterwerte, was bedeutet, dass diese deutlich stärker mit "E_AV_Lab" korreliert sind, als mit den anderen Werten.

Nichtnegative Matrixfaktorisierung (NMF)

Methode

Matrixfaktorisierung wird genutzt, um die Anzahl der Beobachtungen (die Anzahl der Variablen bleibt gleich) zu reduzieren. Dabei zerteilt man einen Datensatz in zwei niedrigdimensionale Matrizen. Das ist sinnvoll, wenn man die Daten komprimieren oder latente Merkmale extrahieren möchte. Es wird z.B. bei der Bilderkennung benutzt, aber auch als Alternative zum Clustering, wenn keine klaren Cluster erkennbar sind.

Die nichtnegative Matrixfaktorisierung ist der typischste Ansatz, wobei alle Elemente Matrizen nicht-negativ sind (sein müssen). Dies ist besonders nützlich für Anwendungen, bei denen die Daten nicht-negativ sind, wie z.B. Bilder, Texte und Empfehlungssysteme. Gegeben ist die nicht negative Matrix $\boldsymbol{X}$ mit Dimension $m × n$ welche wir in die zwei Matritzen $\boldsymbol{W}$ und $\boldsymbol{H}$ mit der Dimension $m×k$ und $k×n$ zerlegen wollen, so dass

$$ \boldsymbol{X} \approx \boldsymbol{W} \boldsymbol{H}. $$

wobei $k$ die Anzahl der latenten Merkmale ist.

Wir wollen $W$ und $H$ finden, so dass die Differenz zwischen $\boldsymbol{X}$ und $\boldsymbol{W} \boldsymbol{H}$ minimiert wird. Wir minimieren hierfür wieder den quadratischen Fehler

$$ \displaystyle \min_{\boldsymbol{W}, \boldsymbol{H}} (\boldsymbol{X} - \boldsymbol{W} \boldsymbol{H})^2​ $$

Eine gebräuchliche Methode dafür ist der folgende iterative Algorithmus:

Schritt 1 - Initialisiere: Initialisiere $\boldsymbol{W}$ und $\boldsymbol{H}$ mit zufälligen nicht-negativen Werten.

Schritt 2 - Iterative Aktualisierung: Aktualisiere $\boldsymbol{W}$ und $\boldsymbol{H}$ iterativ unter Verwendung der multiplikativen Aktualisierungsregeln:

$$ \boldsymbol{H} \leftarrow \boldsymbol{H} \odot \frac{\boldsymbol{W}^T \boldsymbol{X}}{\boldsymbol{W}^T \boldsymbol{W} \boldsymbol{H}} $$

$$ \boldsymbol{W} \leftarrow \boldsymbol{W} \odot \frac{\boldsymbol{X} \boldsymbol{H}^T}{\boldsymbol{W} \boldsymbol{H} \boldsymbol{H}^T} $$

wobei $\odot$ das elementweise Produkt und $\frac{A}{B}​$ die elementweise Division bezeichnet.

Schritt 3 - Konvergenzkriterium: Überprüfe die Konvergenz, z.B. ob die Änderung des Rekonstruktionsfehlers unter einen bestimmten Schwellenwert fällt oder eine maximale Anzahl von Iterationen erreicht ist.

Schritt 4 - Rekonstruktion: Die rekonstruierte Matrix $\boldsymbol{\hat X}$ ist das Produkt der Faktormatrizen $\boldsymbol{W}$ und $\boldsymbol{H}$:

$$ \boldsymbol{\hat X} = \boldsymbol{W} \boldsymbol{H}. $$

NMF in SciKit-Learn

Auch für die nicht-negative Matrixfaktorisierung gibt es eine Implementation in sklearn. Zu beachten ist, dass sie allerdings nur nicht-negative Werte verarbeiten kann. Deshalb müssen wir unsere Daten zuerst auf einen positiven Wertebereich normalisieren. Dafür können wir den MinMaxSkaler verwenden, der unsere Daten auf den Wertebereich $0,\ldots,1$ transformiert.

$$ \boldsymbol X_\text{mx}​ =\frac{\boldsymbol X − \boldsymbol \min_X}{\boldsymbol \max_X - \boldsymbol \min_X}. $$

mit dem Vektor der minimalen Werte $\boldsymbol \min_X$ und maximalen Werte $\boldsymbol \max_X$ aller Variablen in $\boldsymbol X$.

from sklearn.preprocessing import MinMaxScaler

mms = MinMaxScaler()
egywthMinMax = mms.fit_transform(egywthNumber)
mms.min_, mms.scale_

(array([  0.        ,  -0.14705882,  -0.17349138,  -0.19689119,
          0.        ,  -0.14126394,  -0.08982036,   0.        ,
          0.        ,   0.        ,   0.        ,   0.        ,
         -0.13333333, -14.3641576 ,   0.1627907 ,  -0.55099483,
          0.09004739,   0.28315412,   0.415625  ]),
 array([0.00022624, 0.00022624, 0.00053879, 0.00259067, 0.00847458,
        0.03717472, 0.05988024, 0.02427184, 0.125     , 0.06198475,
        0.08333333, 0.125     , 0.05128205, 0.01470156, 0.02906977,
        0.01566661, 0.02369668, 0.03584229, 0.03125   ]))

Die Anwendung der NMF ist nun einfach.

from sklearn.decomposition import NMF

nmfm = NMF(n_components=2)
W = nmfm.fit_transform(egywthMinMax)
H = nmfm.components_

Hier gibt nun die Matrix $W$ aus welchen Komponenten sich jede Beobachtung in unserem Datensatz zusammensetzt. Zum Beispiel sehen wir, dass die ersten zwei Zeilen sich nur aus der Komponente 1 zusammensetzen.

pd.DataFrame(W, columns=[f'Merkmal {i+1}' for i in range(n_components)])

	Merkmal 1	Merkmal 2
0	0.237477	0.000000
1	0.241596	0.000000
2	0.223237	0.016886
3	0.222422	0.028341
4	0.252235	0.000574
...	...	...
911	0.202307	0.057166
912	0.186173	0.083753
913	0.200195	0.037590
914	0.209245	0.025975
915	0.205023	0.028051

916 rows × 2 columns

Interessanter ist die Matrix $H$, weil sie die extrahierten Komponenten darstellen. Hierfür transformieren wir sie zurück in den originalen Datenbereich in dem wir den MinMaxScaler mit inverse_transform anwenden.

H_rescaled=mms.inverse_transform(H)
pd.DataFrame(H_rescaled, columns=egywthNumber.columns)

	EV_HT_740	EV_NT_740	E_AV_Lab	E_SV_Lab	ES_Lab	FX	FM	RSK	RSKF	SDK	SHK_TAG	NM	VPM	PM	TMK	UPM	TXK	TNK	TGK
0	5016.697406	10212.326793	3809.19813	881.823074	0.000000	45.343953	18.038292	12.541693	30.164496	0.000000	1.338495	33.113833	23.604693	1102.063064	36.801254	244.265681	37.890283	37.097455	50.788804
1	2445.902565	4540.833326	2136.22941	468.661514	199.960004	14.237872	5.890776	0.000000	0.000000	26.505994	0.000000	4.171526	25.429733	1063.255817	42.593383	91.811460	50.407605	36.071585	35.274881

Diese zwei Komponenten sind nun die zwei Kombinationen, welche den Datensatz am besten erklären. So lassen sich aus großen Datensätze wichtige Kombinationen ableiten. Man kann sie ähnlich wie Cluster-Zentren auffassen.

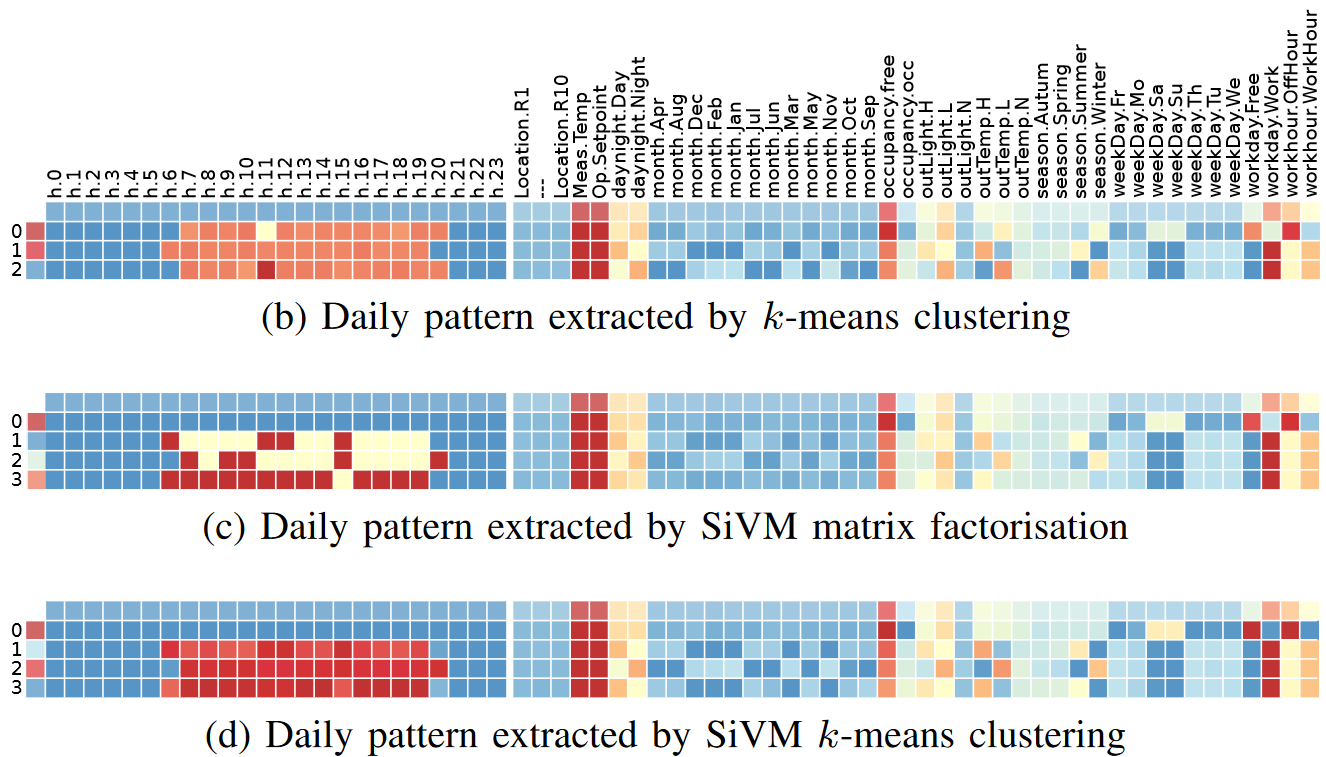
Die folgende Abbildung aus der Publikation "Understanding building operation from semantic context" {cite:p}Ploennigs15 zeigt das in einem Beispiel. In der Publikation wird die Steuerungsstragien von Gebäuden aus den Verbrauchsdaten ableitet. Die Abbildung vergleicht dabei die Muster die durch Clustering ($k$-Means), SiVM-Matrix-Faktorisierung (vergleichbar mit NMF die insbesondere charakteristische Muster identifiziert) und SiVM-Clustering (eine Kombination beider) identifiziert werden. Hierbei zeigt sich, dass die Muster, die durch SiVM-Matrix-Faktorisierung identifiziert werden deutlich ausgeprägter sind, was an der besonderen Methode SiVM liegt, zur Identifikation der Komponenten. Daraus wurden dann wieder Betriebsregeln abgeleitet durch Assoziationsanalyse, welches Entscheidungsbäumen ähneln.

f  r  a  g  e  n  ?