Klassifikation

Den Wald vor lauter Bäumen nicht sehen

— Christoph Martin Wieland

Die Klassifikation ist die zweite wichtige Problemstellung im Supervised Learning deren Ziel es ist für eine Menge an Daten vorher bekannte Klassen zu lernen und diese für neue Datensätze vorherzusagen. Bei den Klassen kann es sich um binäre Daten handeln (z.B. Ja/Nein - Erkennung, ob ein Bauteil intakt oder beschädigt ist, Ein/Aus - Aktivität von Anlagen) oder kategorische Daten (z.B. Kategorisierung von Rissen: fein, mittel, grob). Sie können aber auch zur Klassifikation genutzt werden – auch wenn die mathematische Struktur Regressionsmodellen ähnelt - genauso wie logistische Regressionsmodelle, die speziell für binäre Klassifikation gedacht sind verwendet werden können.

Klassifikationsmodelle werden in der Praxis häufig zur Erkennung von Spam eingesetzt (Ja/Nein), Betrugserkennung, Anomalieerkennung, Kreditratings oder Allgemein für Vorhersageprobleme. Es gibt verschiedene Arten von Klassifikationsmodellen, von denen wir einige typische Ansätze diskutieren wollen.

Folien

Entscheidungsbäume zur Klassifikation

Entscheidungsbäume (en. Decission Trees) sind eine beliebte Methode des maschinellen Lernens zur Klassifizierung von Datenpunkten, da sie intuitiv und leicht verständlich sind. Das macht sie zu einem guten Werkzeug für Anfänger und Experten gleichermaßen. Sie können numerische und kategorische Daten als Eingangsvariablen verarbeiten.

Das Grundelement eines Entscheidungsbaum ist eine einfache Wenn-Dann-Sonst-Verzweigung (if-else), die wir aus der Programmierung kennen. Hierbei wird auf einer Eingangsgrößen eine Bedingung definiert und für die beiden Antwortvarianten werden unterschiedliche Rückgabewerte ausgegeben.

if x > 30:
  y = "Cool"
else:
  if x < 18:
    y = "Heat"
  else:
    y = "off"

Durch Verschachteln der Bedingungen entsteht eine Baumstruktur, die wir in einem Flussdiagramm darstellen können. Das Flussdiagramm besteht aus Knoten, Kanten und Blättern:

• Knoten: Ein Punkt im Baum, an dem eine Entscheidung getroffen wird, basierend auf einem Eingangswert.

• Kanten: Verbindungen zwischen den Knoten, die den Entscheidungsfluss darstellen.

• Blätter: Endknoten des Baumes, die eine Klassifikation oder Vorhersage darstellen.

Durch diesen einfachen Aufbau ist ein Entscheidungsbaum bis zu einer gewissen Tiefe gut erklärbar, da man für jeden Eingangswert die entsprechende Entscheidungskette im Baum nachvollziehen kann. Deshalb werden Entscheidungsbäume auch beim Data Mining genutzt, um bisher unbekannte Regeln aus einem Datensatz abzuleiten.

Ferner ist der Baum bei der Vorhersage (Scoring) sehr effizient zu berechnen, da auch bei vielen Bedingungen durch die Baumstruktur nur ein kleiner Teil an relevanten Bedingungen betrachtet werden muss (log(n)-Komplexität).

Erstellen eines Entscheidungsbaums

Sind die Regeln bekannt, kann der Entscheidungsbaum, wie im obigen Beispiel gezeigm, manuell definiert werden. Im Machine Learning besteht allerdings die Zielstellung diesen Entscheidungsbaum automatisch aus den Trainingsdaten abzuleiten. Das geschieht in drei Schritten:

1. Auswahl des besten Attributs zur Trennung der Daten.

2. Aufteilung des Datensatzes basierend auf dem ausgewählten Attribut.

3. Wiederholung des Prozesses für jeden Teilbaum, bis ein Abbruchkriterium erfüllt ist.

Auswahl des besten Attributes

Die Auswahl des besten Attributs erfolgt typischerweise durch Maximierung eines Kriteriums wie dem Informationsgewinn oder der Gini-Impurity.

Informationsgewinn: Der Informationsgewinn basiert auf dem Konzept der Entropie. Die Entropie misst wie viel Zufall eine Variable enthält und ist somit ein Varianzmaß. Die Entropie \(H(S)\) einer Variable \(S\) wird wie folgt berechnet:

\[ H(S) = - \sum_{k=1}^{c} p_k \log_2(p_k) \]

wobei \(c\) die Anzahl der Klassen und \(p_k\) der Anteil der Klasse \(k\) im Datensatz \(S\) ist.

Der Informationsgewinn \(IG(T, A)\) eines Attributs \(A\) für den Datensatz \(T\) wird dann berechnet als:

\[ \overbrace{IG(T, A)}^\text{Informationsgewinn} = \overbrace{H(T)}^\text{Entropy des Knoten} - \overbrace{\sum_{v \in Values(A)} \frac{|T_v|}{|T|} H(T_v)}^\text{Entropy aller Subknoten} \]

wobei \(Values(A)\) die möglichen Werte von Attribut \(A\) sind und \(T_v\) der Teil des Datensatzes \(T\) ist, bei dem Attribut \(A\) den Wert \(v\) hat. Der Informationsgewinn misst somit wie viel Entropie ein Knoten zu dem finalen Datensatz beiträgt.

Gini-Impurity: Die Gini-Impurity eines Datensatzes \(S\) wird wie folgt berechnet:

\[ Gini(S) = 1 - \sum_{i=1}^{c} p_i^2 \]

Der Gini-Gewinn wird ähnlich wie der Informationsgewinn berechnet, wobei anstelle der Entropie die Gini-Impurity verwendet wird.

Beispiel

Betrachten wir ein einfaches Beispiel zur Veranschaulichung. Angenommen, wir haben den obigen Datensatz mit den Klassen “Apfel” und “Orange” und den Attributen “Farbe” und “Größe”. Unser Ziel ist es, einen Entscheidungsbaum zu erstellen, der die Früchte klassifiziert.

Berechnung der Entropie des gesamten Datensatzes

Entsprechend der obigen Abbildung enthält der Datensatz 4 Äpfel und 5 Orangen. Die Entropie des gesamten Datensatzes ist folglich:

\[ H(S) = - \left( \frac{5}{9} \log_2 \frac{5}{9} + \frac{4}{9} \log_2 \frac{4}{9} \right) = 0.99 \]

Berechnung der Entropie für jedes Attribut

Wir berechnen nun für jeden möglichen Split der Daten den resultierenden Informationsgewinn. Wir haben können den Datensatz anhand des Attributs Farbe splitten oder anhand des Attributs Größe. Splitten wir den Datensatz auf Basis der Farbe so haben wir 5 Objekte mit der Farbe “orange” und 4 mit der Farbe “rot”.

Wir berechnen die Entropie nach der Aufteilung auf Basis der Farbe:

(6)\[\begin{align} H(Farbe=Rot) &= - \left( \frac{1}{5} \log_2 \frac{1}{5} + \frac{4}{5} \log_2 \frac{4}{5} \right) &= 0.72 \\ H(Farbe=Orange) &= - \left( \frac{4}{4} \log_2 \frac{4}{4} \right) &= 0.0 \\ IG(Farbe) &= H(S) - \frac{5}{9} H(Farbe=Rot) - \frac{4}{9} H(Farbe=Orange) \\ &= 0.99 - \frac{5}{9} 0.72 - \frac{4}{9} 0.0 &= 0.59 \end{align}\]

Jetzt berechnen wir die Entropie nach der Aufteilung auf Basis der Größe:

(7)\[\begin{align} H(Größe=Klein) &= - \left( \frac{2}{5} \log_2 \frac{2}{5} + \frac{3}{5} \log_2 \frac{3}{5} \right) &= 0.97 \\ H(Größe=Gross) &= - \left( \frac{2}{4} \log_2 \frac{2}{4} + \frac{2}{4} \log_2 \frac{2}{4} \right) &= 1.0 \\ IG(Größe) &= H(S) - \frac{5}{9} H(Größe=Klein) - \frac{4}{9} H(Größe=Gross) \\ &= 0.99 - \frac{5}{9} 0.97 - \frac{4}{9} 1.0 &= 0.01 \end{align}\]

Es zeigt sich, dass der Informationsgewinn bei der \(Farbe\) deutlich höher ist als bei der \(Größe\), weshalb es sinnvoll ist diesen als ersten Knoten im Entscheidungsbaum zu wählen.

Entscheidungsbäume in SciKit-Learn

Entscheidungsbäume können unter andrem mit SciKit-Learn erstellt werden. Hierfür erstellen wir wie gewohnt eine Modellklasse und können dabei auch das Kriterium angeben

from sklearn.tree import DecisionTreeClassifier

clf = DecisionTreeClassifier(criterion="entropy")

---------------------------------------------------------------------------
ImportError                               Traceback (most recent call last)
File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/__init__.py:24
     23 try:
---> 24     from . import multiarray
     25 except ImportError as exc:

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/multiarray.py:10
      9 import functools
---> 10 from . import overrides
     11 from . import _multiarray_umath

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/overrides.py:8
      7 from .._utils._inspect import getargspec
----> 8 from numpy.core._multiarray_umath import (
      9     add_docstring,  _get_implementing_args, _ArrayFunctionDispatcher)
     12 ARRAY_FUNCTIONS = set()

ImportError: dlopen(/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/_multiarray_umath.cpython-311-darwin.so, 0x0002): Library not loaded: @rpath/libgfortran.5.dylib
  Referenced from: <342C6FCD-A261-33D7-B978-626161CFD49B> /opt/miniconda3/envs/lehre/lib/libopenblas.0.dylib
  Reason: tried: '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/usr/local/lib/libgfortran.5.dylib' (no such file), '/usr/lib/libgfortran.5.dylib' (no such file, not in dyld cache)

During handling of the above exception, another exception occurred:

ImportError                               Traceback (most recent call last)
File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__init__.py:130
    129 try:
--> 130     from numpy.__config__ import show as show_config
    131 except ImportError as e:

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__config__.py:4
      3 from enum import Enum
----> 4 from numpy.core._multiarray_umath import (
      5     __cpu_features__,
      6     __cpu_baseline__,
      7     __cpu_dispatch__,
      8 )
     10 __all__ = ["show"]

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/__init__.py:50
     27     msg = """
     28 
     29 IMPORTANT: PLEASE READ THIS FOR ADVICE ON HOW TO SOLVE THIS ISSUE!
   (...)
     48 """ % (sys.version_info[0], sys.version_info[1], sys.executable,
     49         __version__, exc)
---> 50     raise ImportError(msg)
     51 finally:

ImportError: 

IMPORTANT: PLEASE READ THIS FOR ADVICE ON HOW TO SOLVE THIS ISSUE!

Importing the numpy C-extensions failed. This error can happen for
many reasons, often due to issues with your setup or how NumPy was
installed.

We have compiled some common reasons and troubleshooting tips at:

    https://numpy.org/devdocs/user/troubleshooting-importerror.html

Please note and check the following:

  * The Python version is: Python3.11 from "/opt/miniconda3/envs/lehre/bin/python"
  * The NumPy version is: "1.26.4"

and make sure that they are the versions you expect.
Please carefully study the documentation linked above for further help.

Original error was: dlopen(/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/_multiarray_umath.cpython-311-darwin.so, 0x0002): Library not loaded: @rpath/libgfortran.5.dylib
  Referenced from: <342C6FCD-A261-33D7-B978-626161CFD49B> /opt/miniconda3/envs/lehre/lib/libopenblas.0.dylib
  Reason: tried: '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/usr/local/lib/libgfortran.5.dylib' (no such file), '/usr/lib/libgfortran.5.dylib' (no such file, not in dyld cache)


The above exception was the direct cause of the following exception:

ImportError                               Traceback (most recent call last)
Cell In[1], line 1
----> 1 from sklearn.tree import DecisionTreeClassifier
      3 clf = DecisionTreeClassifier(criterion="entropy")

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/sklearn/__init__.py:73
     62 # `_distributor_init` allows distributors to run custom init code.
     63 # For instance, for the Windows wheel, this is used to pre-load the
     64 # vcomp shared library runtime for OpenMP embedded in the sklearn/.libs
   (...)
     67 # later is linked to the OpenMP runtime to make it possible to introspect
     68 # it and importing it first would fail if the OpenMP dll cannot be found.
     69 from . import (  # noqa: F401 E402
     70     __check_build,
     71     _distributor_init,
     72 )
---> 73 from .base import clone  # noqa: E402
     74 from .utils._show_versions import show_versions  # noqa: E402
     76 _submodules = [
     77     "calibration",
     78     "cluster",
   (...)
    114     "compose",
    115 ]

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/sklearn/base.py:14
     11 import warnings
     12 from collections import defaultdict
---> 14 import numpy as np
     16 from . import __version__
     17 from ._config import config_context, get_config

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__init__.py:135
    131 except ImportError as e:
    132     msg = """Error importing numpy: you should not try to import numpy from
    133     its source directory; please exit the numpy source tree, and relaunch
    134     your python interpreter from there."""
--> 135     raise ImportError(msg) from e
    137 __all__ = [
    138     'exceptions', 'ModuleDeprecationWarning', 'VisibleDeprecationWarning',
    139     'ComplexWarning', 'TooHardError', 'AxisError']
    141 # mapping of {name: (value, deprecation_msg)}

ImportError: Error importing numpy: you should not try to import numpy from
        its source directory; please exit the numpy source tree, and relaunch
        your python interpreter from there.

Erstellen wir uns als nächstes den Beispieldatensatz as Pandas Dataframe

import numpy as np # Import von NumPy
import pandas as pd # Import von Pandas
df=pd.DataFrame([
    ["Orange","Gross","Orange"],
    ["Rot","Gross","Orange"],
    ["Rot","Gross","Apfel"],
    ["Orange","Klein","Orange"],
    ["Orange","Klein","Orange"],
    ["Rot","Klein","Apfel"],
    ["Rot","Klein","Apfel"],
    ["Rot","Gross","Apfel"],
    ["Orange","Klein","Orange"]
],columns=["Color","Size","Typ"])
df

---------------------------------------------------------------------------
ImportError                               Traceback (most recent call last)
File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/__init__.py:24
     23 try:
---> 24     from . import multiarray
     25 except ImportError as exc:

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/multiarray.py:10
      9 import functools
---> 10 from . import overrides
     11 from . import _multiarray_umath

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/overrides.py:8
      7 from .._utils._inspect import getargspec
----> 8 from numpy.core._multiarray_umath import (
      9     add_docstring,  _get_implementing_args, _ArrayFunctionDispatcher)
     12 ARRAY_FUNCTIONS = set()

ImportError: dlopen(/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/_multiarray_umath.cpython-311-darwin.so, 0x0002): Library not loaded: @rpath/libgfortran.5.dylib
  Referenced from: <342C6FCD-A261-33D7-B978-626161CFD49B> /opt/miniconda3/envs/lehre/lib/libopenblas.0.dylib
  Reason: tried: '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/usr/local/lib/libgfortran.5.dylib' (no such file), '/usr/lib/libgfortran.5.dylib' (no such file, not in dyld cache)

During handling of the above exception, another exception occurred:

ImportError                               Traceback (most recent call last)
File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__init__.py:130
    129 try:
--> 130     from numpy.__config__ import show as show_config
    131 except ImportError as e:

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__config__.py:4
      3 from enum import Enum
----> 4 from numpy.core._multiarray_umath import (
      5     __cpu_features__,
      6     __cpu_baseline__,
      7     __cpu_dispatch__,
      8 )
     10 __all__ = ["show"]

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/__init__.py:50
     27     msg = """
     28 
     29 IMPORTANT: PLEASE READ THIS FOR ADVICE ON HOW TO SOLVE THIS ISSUE!
   (...)
     48 """ % (sys.version_info[0], sys.version_info[1], sys.executable,
     49         __version__, exc)
---> 50     raise ImportError(msg)
     51 finally:

ImportError: 

IMPORTANT: PLEASE READ THIS FOR ADVICE ON HOW TO SOLVE THIS ISSUE!

Importing the numpy C-extensions failed. This error can happen for
many reasons, often due to issues with your setup or how NumPy was
installed.

We have compiled some common reasons and troubleshooting tips at:

    https://numpy.org/devdocs/user/troubleshooting-importerror.html

Please note and check the following:

  * The Python version is: Python3.11 from "/opt/miniconda3/envs/lehre/bin/python"
  * The NumPy version is: "1.26.4"

and make sure that they are the versions you expect.
Please carefully study the documentation linked above for further help.

Original error was: dlopen(/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/_multiarray_umath.cpython-311-darwin.so, 0x0002): Library not loaded: @rpath/libgfortran.5.dylib
  Referenced from: <342C6FCD-A261-33D7-B978-626161CFD49B> /opt/miniconda3/envs/lehre/lib/libopenblas.0.dylib
  Reason: tried: '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/usr/local/lib/libgfortran.5.dylib' (no such file), '/usr/lib/libgfortran.5.dylib' (no such file, not in dyld cache)


The above exception was the direct cause of the following exception:

ImportError                               Traceback (most recent call last)
Cell In[2], line 1
----> 1 import numpy as np # Import von NumPy
      2 import pandas as pd # Import von Pandas
      3 df=pd.DataFrame([
      4     ["Orange","Gross","Orange"],
      5     ["Rot","Gross","Orange"],
   (...)
     12     ["Orange","Klein","Orange"]
     13 ],columns=["Color","Size","Typ"])

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__init__.py:135
    131 except ImportError as e:
    132     msg = """Error importing numpy: you should not try to import numpy from
    133     its source directory; please exit the numpy source tree, and relaunch
    134     your python interpreter from there."""
--> 135     raise ImportError(msg) from e
    137 __all__ = [
    138     'exceptions', 'ModuleDeprecationWarning', 'VisibleDeprecationWarning',
    139     'ComplexWarning', 'TooHardError', 'AxisError']
    141 # mapping of {name: (value, deprecation_msg)}

ImportError: Error importing numpy: you should not try to import numpy from
        its source directory; please exit the numpy source tree, and relaunch
        your python interpreter from there.

Hier ist wieder zu beachten das SciKit-Learn nicht direkt auf kategorischen Spalten mit Text arbeitet, sondern binäre oder numerische Spalten erwartet. Wir können binäre Variablen mit der Methode get_dummies erzeugen:

dfD= pd.get_dummies(df,columns=["Color","Size","Typ"],drop_first=False)
dfD.head(2)

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[3], line 1
----> 1 dfD= pd.get_dummies(df,columns=["Color","Size","Typ"],drop_first=False)
      2 dfD.head(2)

NameError: name 'pd' is not defined

Oder alternativ numerische Variablen mit der Funktion pd.factorize erzeugen. Das bietet sich hier mehr an, da es eine kompaktere Darstellung ist

dfF=df.copy()
dfF["Color"], df_map_col = pd.factorize(df["Color"])
dfF["Size"], df_map_size = pd.factorize(df["Size"])
dfF["Typ"], df_map_typ = pd.factorize(df["Typ"])
dfF, df_map_col, df_map_size, df_map_typ

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[4], line 1
----> 1 dfF=df.copy()
      2 dfF["Color"], df_map_col = pd.factorize(df["Color"])
      3 dfF["Size"], df_map_size = pd.factorize(df["Size"])

NameError: name 'df' is not defined

Mit der Modellmethode fit können wir wieder das Modell trainieren, indem wir die Eingänge x und die Zielvariable y spezifizieren.

x=dfF[['Color','Size']]
y=dfF["Typ"]

clf.fit(x, y)

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[5], line 1
----> 1 x=dfF[['Color','Size']]
      2 y=dfF["Typ"]
      4 clf.fit(x, y)

NameError: name 'dfF' is not defined

Mit der Funktion plot_tree können wir uns den Entscheidungsbaum anzeigen lassen:

from sklearn.tree import plot_tree
import matplotlib.pyplot as plt

plt.figure(figsize=(20,10))
plot_tree(clf, filled=True, feature_names=['Color','Size'], class_names=df_map_typ)
plt.show()

---------------------------------------------------------------------------
ImportError                               Traceback (most recent call last)
File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/__init__.py:24
     23 try:
---> 24     from . import multiarray
     25 except ImportError as exc:

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/multiarray.py:10
      9 import functools
---> 10 from . import overrides
     11 from . import _multiarray_umath

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/overrides.py:8
      7 from .._utils._inspect import getargspec
----> 8 from numpy.core._multiarray_umath import (
      9     add_docstring,  _get_implementing_args, _ArrayFunctionDispatcher)
     12 ARRAY_FUNCTIONS = set()

ImportError: dlopen(/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/_multiarray_umath.cpython-311-darwin.so, 0x0002): Library not loaded: @rpath/libgfortran.5.dylib
  Referenced from: <342C6FCD-A261-33D7-B978-626161CFD49B> /opt/miniconda3/envs/lehre/lib/libopenblas.0.dylib
  Reason: tried: '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/usr/local/lib/libgfortran.5.dylib' (no such file), '/usr/lib/libgfortran.5.dylib' (no such file, not in dyld cache)

During handling of the above exception, another exception occurred:

ImportError                               Traceback (most recent call last)
File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__init__.py:130
    129 try:
--> 130     from numpy.__config__ import show as show_config
    131 except ImportError as e:

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__config__.py:4
      3 from enum import Enum
----> 4 from numpy.core._multiarray_umath import (
      5     __cpu_features__,
      6     __cpu_baseline__,
      7     __cpu_dispatch__,
      8 )
     10 __all__ = ["show"]

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/__init__.py:50
     27     msg = """
     28 
     29 IMPORTANT: PLEASE READ THIS FOR ADVICE ON HOW TO SOLVE THIS ISSUE!
   (...)
     48 """ % (sys.version_info[0], sys.version_info[1], sys.executable,
     49         __version__, exc)
---> 50     raise ImportError(msg)
     51 finally:

ImportError: 

IMPORTANT: PLEASE READ THIS FOR ADVICE ON HOW TO SOLVE THIS ISSUE!

Importing the numpy C-extensions failed. This error can happen for
many reasons, often due to issues with your setup or how NumPy was
installed.

We have compiled some common reasons and troubleshooting tips at:

    https://numpy.org/devdocs/user/troubleshooting-importerror.html

Please note and check the following:

  * The Python version is: Python3.11 from "/opt/miniconda3/envs/lehre/bin/python"
  * The NumPy version is: "1.26.4"

and make sure that they are the versions you expect.
Please carefully study the documentation linked above for further help.

Original error was: dlopen(/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/_multiarray_umath.cpython-311-darwin.so, 0x0002): Library not loaded: @rpath/libgfortran.5.dylib
  Referenced from: <342C6FCD-A261-33D7-B978-626161CFD49B> /opt/miniconda3/envs/lehre/lib/libopenblas.0.dylib
  Reason: tried: '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/usr/local/lib/libgfortran.5.dylib' (no such file), '/usr/lib/libgfortran.5.dylib' (no such file, not in dyld cache)


The above exception was the direct cause of the following exception:

ImportError                               Traceback (most recent call last)
Cell In[6], line 1
----> 1 from sklearn.tree import plot_tree
      2 import matplotlib.pyplot as plt
      4 plt.figure(figsize=(20,10))

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/sklearn/__init__.py:73
     62 # `_distributor_init` allows distributors to run custom init code.
     63 # For instance, for the Windows wheel, this is used to pre-load the
     64 # vcomp shared library runtime for OpenMP embedded in the sklearn/.libs
   (...)
     67 # later is linked to the OpenMP runtime to make it possible to introspect
     68 # it and importing it first would fail if the OpenMP dll cannot be found.
     69 from . import (  # noqa: F401 E402
     70     __check_build,
     71     _distributor_init,
     72 )
---> 73 from .base import clone  # noqa: E402
     74 from .utils._show_versions import show_versions  # noqa: E402
     76 _submodules = [
     77     "calibration",
     78     "cluster",
   (...)
    114     "compose",
    115 ]

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/sklearn/base.py:14
     11 import warnings
     12 from collections import defaultdict
---> 14 import numpy as np
     16 from . import __version__
     17 from ._config import config_context, get_config

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__init__.py:135
    131 except ImportError as e:
    132     msg = """Error importing numpy: you should not try to import numpy from
    133     its source directory; please exit the numpy source tree, and relaunch
    134     your python interpreter from there."""
--> 135     raise ImportError(msg) from e
    137 __all__ = [
    138     'exceptions', 'ModuleDeprecationWarning', 'VisibleDeprecationWarning',
    139     'ComplexWarning', 'TooHardError', 'AxisError']
    141 # mapping of {name: (value, deprecation_msg)}

ImportError: Error importing numpy: you should not try to import numpy from
        its source directory; please exit the numpy source tree, and relaunch
        your python interpreter from there.

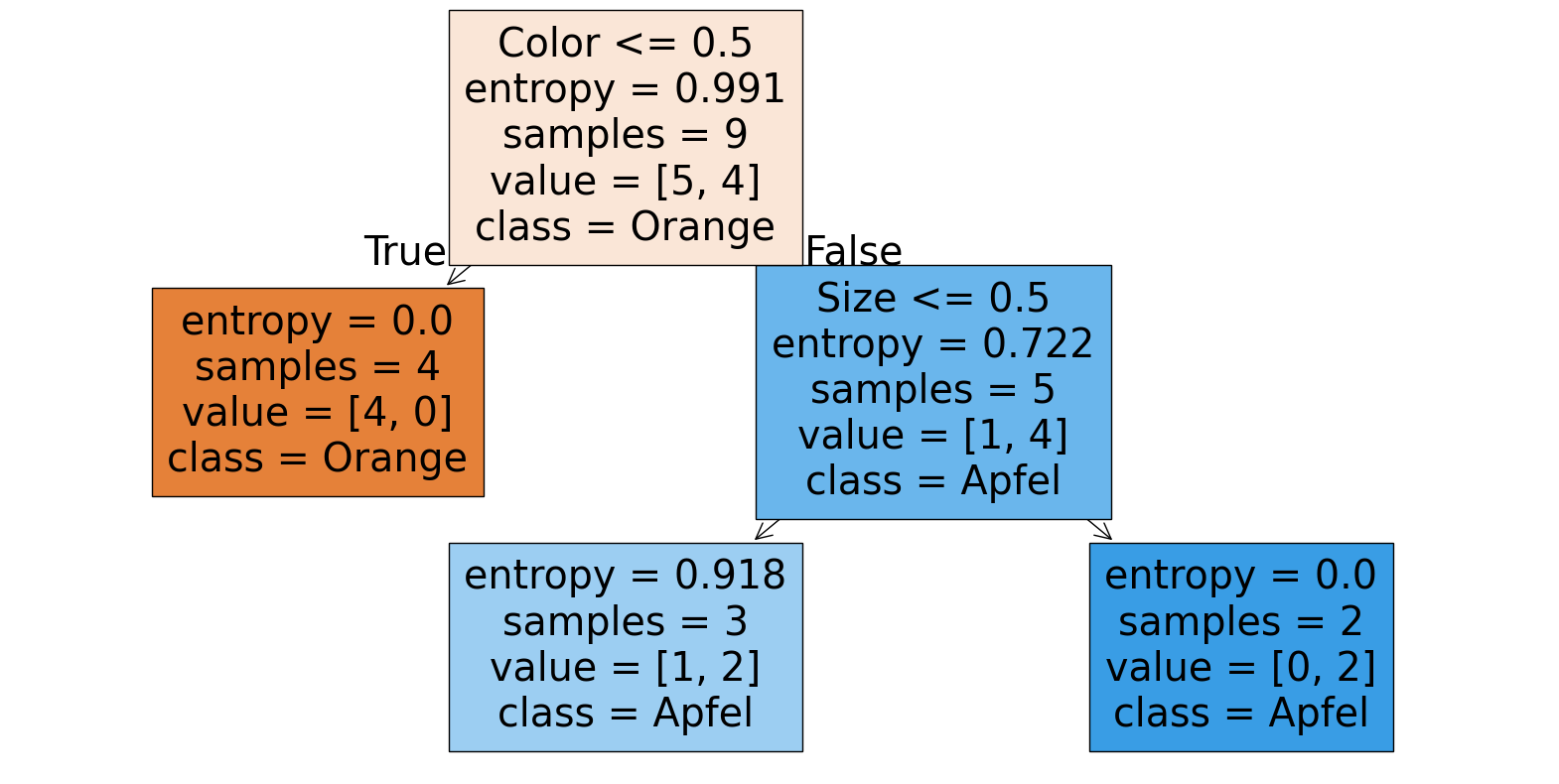
Mit der bekannten Methode predict können wir eine Vorhersage treffen. Also ein Objekt das Orange (0) ist und Klein (1) ist eine Orange (0).

clf.predict([[0,1]])

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[7], line 1
----> 1 clf.predict([[0,1]])

NameError: name 'clf' is not defined

Prüfen wir das Modell einmal an dem uns bekannten Energie- und Wetterdatensatz. Wir laden den Datensatz und fügen eine Spalte für den Wochentag (gleich numerisch) hinzu und ob der EV_HT_740-Verbraucher an ist. Wir brauchen in diesem Fall die fehlenden NaN Werte nicht entfernen.

egywth = pd.read_csv("../data/UROS/Energy1D_weather_clean.csv", parse_dates=[0])
egywth["Weekday"] = egywth["Date"].dt.dayofweek
egywth["EV_HT_740_IS_ON"] = egywth.EV_HT_740==0

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[8], line 1
----> 1 egywth = pd.read_csv("../data/UROS/Energy1D_weather_clean.csv", parse_dates=[0])
      2 egywth["Weekday"] = egywth["Date"].dt.dayofweek
      3 egywth["EV_HT_740_IS_ON"] = egywth.EV_HT_740==0

NameError: name 'pd' is not defined

Wir wollen ein Modell für die Temperaturklasse und den Heiztage und Kühltage bestimmen, um zu sehen ob die originalen Grenzen aus dem Notebook zur Datenvorverarbeitung erkannt werden. Hierfür wandeln wir die Spalten zuerst in Numerische Kategorien um.

egywth["TemperaturKlasseN"], TK_map = pd.factorize(egywth["TemperaturKlasse"])
egywth["HeizKuehlTageN"], HKT_map = pd.factorize(egywth["HeizKuehlTage"])
TK_map,HKT_map

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[9], line 1
----> 1 egywth["TemperaturKlasseN"], TK_map = pd.factorize(egywth["TemperaturKlasse"])
      2 egywth["HeizKuehlTageN"], HKT_map = pd.factorize(egywth["HeizKuehlTage"])
      3 TK_map,HKT_map

NameError: name 'pd' is not defined

Dann trainieren und visualisieren wir die Entscheidungsbäume.

clfTK = DecisionTreeClassifier()
clfTK.fit(egywth[['TMK']], egywth[['TemperaturKlasseN']])
clfTK.get_depth()

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[10], line 1
----> 1 clfTK = DecisionTreeClassifier()
      2 clfTK.fit(egywth[['TMK']], egywth[['TemperaturKlasseN']])
      3 clfTK.get_depth()

NameError: name 'DecisionTreeClassifier' is not defined

plt.figure(figsize=(20,10))
plot_tree(clfTK, filled=True, feature_names=['TMK'], class_names=TK_map)
plt.show()

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[11], line 1
----> 1 plt.figure(figsize=(20,10))
      2 plot_tree(clfTK, filled=True, feature_names=['TMK'], class_names=TK_map)
      3 plt.show()

NameError: name 'plt' is not defined

clfHKT = DecisionTreeClassifier()
clfHKT.fit(egywth[['TMK']], egywth[['HeizKuehlTageN']])
clfHKT.get_depth()

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[12], line 1
----> 1 clfHKT = DecisionTreeClassifier()
      2 clfHKT.fit(egywth[['TMK']], egywth[['HeizKuehlTageN']])
      3 clfHKT.get_depth()

NameError: name 'DecisionTreeClassifier' is not defined

plt.figure(figsize=(20,10))
plot_tree(clfHKT, filled=True, feature_names=['TMK'], class_names=HKT_map)
plt.show()

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[13], line 1
----> 1 plt.figure(figsize=(20,10))
      2 plot_tree(clfHKT, filled=True, feature_names=['TMK'], class_names=HKT_map)
      3 plt.show()

NameError: name 'plt' is not defined

Es zeigt sich, dass die originalen Grenzen und die Folge der Werte durchaus gut identifiziert werden, wenn auch nicht ganz präzise, da entsprechende Samples im Datensatz fehlen.

Trainieren wir einen Entscheidungsbaum für die Aktivität des EV_HT_740-Verbrauches, wie bei der logistischen Regression.

clfHT = DecisionTreeClassifier()
clfHT.fit(egywth[["SDK", "NM", "VPM", "TMK", "Weekday"]], egywth[['EV_HT_740_IS_ON']])
clfHT.get_depth()

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[14], line 1
----> 1 clfHT = DecisionTreeClassifier()
      2 clfHT.fit(egywth[["SDK", "NM", "VPM", "TMK", "Weekday"]], egywth[['EV_HT_740_IS_ON']])
      3 clfHT.get_depth()

NameError: name 'DecisionTreeClassifier' is not defined

plt.figure(figsize=(20,10))
plot_tree(clfHT, filled=True, feature_names=["SDK", "NM", "VPM", "TMK", "Weekday"], class_names=['Off',"On"])
plt.show()

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[15], line 1
----> 1 plt.figure(figsize=(20,10))
      2 plot_tree(clfHT, filled=True, feature_names=["SDK", "NM", "VPM", "TMK", "Weekday"], class_names=['Off',"On"])
      3 plt.show()

NameError: name 'plt' is not defined

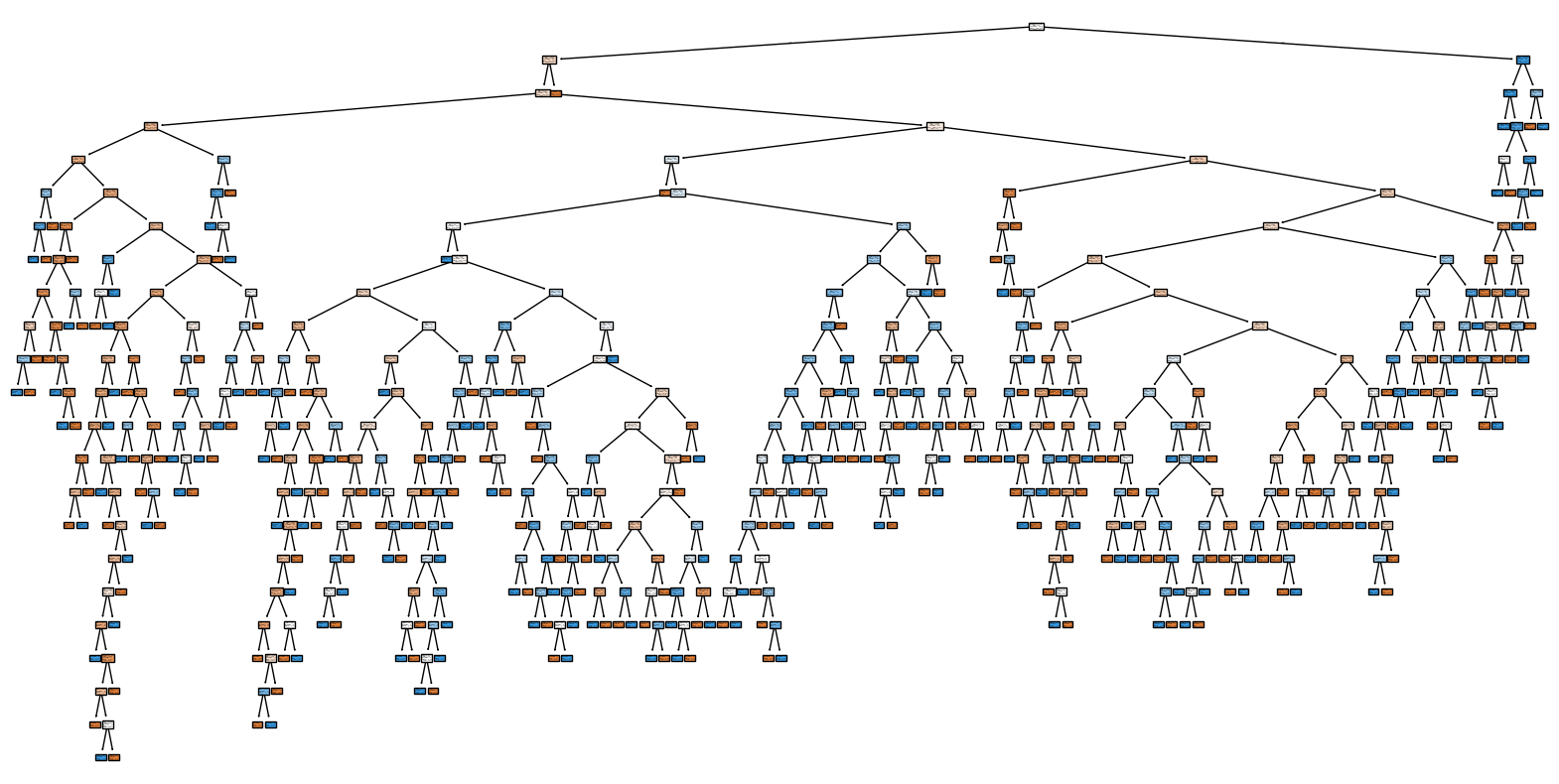
Das resultiert in einen deutlich komplexeren Entscheidungsbaum mit einer Tiefe von 21 Knoten.

Prüfen wir einmal die Vorhersagequalität, indem wir den Trainingsdatensatz vorhersagen.

egywth["pred_DT"] = clfHT.predict(egywth[["SDK", "NM", "VPM", "TMK", "Weekday"]])

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[16], line 1
----> 1 egywth["pred_DT"] = clfHT.predict(egywth[["SDK", "NM", "VPM", "TMK", "Weekday"]])

NameError: name 'clfHT' is not defined

Als Vergleichsmetriken für Entscheidungsbäume die kategorische Werte vorhersagen, verwendet man die Metriken, die wir für die Logistische Regression diskutiert haben.

from sklearn.metrics import accuracy_score, f1_score

print('Accuracy: {:.2f}'.format(accuracy_score(egywth.EV_HT_740_IS_ON.values, egywth.pred_DT)))
print('F1-Score: {:.2f}'.format(f1_score(egywth.EV_HT_740_IS_ON, egywth.pred_DT)))

---------------------------------------------------------------------------
ImportError                               Traceback (most recent call last)
File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/__init__.py:24
     23 try:
---> 24     from . import multiarray
     25 except ImportError as exc:

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/multiarray.py:10
      9 import functools
---> 10 from . import overrides
     11 from . import _multiarray_umath

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/overrides.py:8
      7 from .._utils._inspect import getargspec
----> 8 from numpy.core._multiarray_umath import (
      9     add_docstring,  _get_implementing_args, _ArrayFunctionDispatcher)
     12 ARRAY_FUNCTIONS = set()

ImportError: dlopen(/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/_multiarray_umath.cpython-311-darwin.so, 0x0002): Library not loaded: @rpath/libgfortran.5.dylib
  Referenced from: <342C6FCD-A261-33D7-B978-626161CFD49B> /opt/miniconda3/envs/lehre/lib/libopenblas.0.dylib
  Reason: tried: '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/usr/local/lib/libgfortran.5.dylib' (no such file), '/usr/lib/libgfortran.5.dylib' (no such file, not in dyld cache)

During handling of the above exception, another exception occurred:

ImportError                               Traceback (most recent call last)
File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__init__.py:130
    129 try:
--> 130     from numpy.__config__ import show as show_config
    131 except ImportError as e:

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__config__.py:4
      3 from enum import Enum
----> 4 from numpy.core._multiarray_umath import (
      5     __cpu_features__,
      6     __cpu_baseline__,
      7     __cpu_dispatch__,
      8 )
     10 __all__ = ["show"]

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/__init__.py:50
     27     msg = """
     28 
     29 IMPORTANT: PLEASE READ THIS FOR ADVICE ON HOW TO SOLVE THIS ISSUE!
   (...)
     48 """ % (sys.version_info[0], sys.version_info[1], sys.executable,
     49         __version__, exc)
---> 50     raise ImportError(msg)
     51 finally:

ImportError: 

IMPORTANT: PLEASE READ THIS FOR ADVICE ON HOW TO SOLVE THIS ISSUE!

Importing the numpy C-extensions failed. This error can happen for
many reasons, often due to issues with your setup or how NumPy was
installed.

We have compiled some common reasons and troubleshooting tips at:

    https://numpy.org/devdocs/user/troubleshooting-importerror.html

Please note and check the following:

  * The Python version is: Python3.11 from "/opt/miniconda3/envs/lehre/bin/python"
  * The NumPy version is: "1.26.4"

and make sure that they are the versions you expect.
Please carefully study the documentation linked above for further help.

Original error was: dlopen(/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/_multiarray_umath.cpython-311-darwin.so, 0x0002): Library not loaded: @rpath/libgfortran.5.dylib
  Referenced from: <342C6FCD-A261-33D7-B978-626161CFD49B> /opt/miniconda3/envs/lehre/lib/libopenblas.0.dylib
  Reason: tried: '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/usr/local/lib/libgfortran.5.dylib' (no such file), '/usr/lib/libgfortran.5.dylib' (no such file, not in dyld cache)


The above exception was the direct cause of the following exception:

ImportError                               Traceback (most recent call last)
Cell In[17], line 1
----> 1 from sklearn.metrics import accuracy_score, f1_score
      3 print('Accuracy: {:.2f}'.format(accuracy_score(egywth.EV_HT_740_IS_ON.values, egywth.pred_DT)))
      4 print('F1-Score: {:.2f}'.format(f1_score(egywth.EV_HT_740_IS_ON, egywth.pred_DT)))

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/sklearn/__init__.py:73
     62 # `_distributor_init` allows distributors to run custom init code.
     63 # For instance, for the Windows wheel, this is used to pre-load the
     64 # vcomp shared library runtime for OpenMP embedded in the sklearn/.libs
   (...)
     67 # later is linked to the OpenMP runtime to make it possible to introspect
     68 # it and importing it first would fail if the OpenMP dll cannot be found.
     69 from . import (  # noqa: F401 E402
     70     __check_build,
     71     _distributor_init,
     72 )
---> 73 from .base import clone  # noqa: E402
     74 from .utils._show_versions import show_versions  # noqa: E402
     76 _submodules = [
     77     "calibration",
     78     "cluster",
   (...)
    114     "compose",
    115 ]

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/sklearn/base.py:14
     11 import warnings
     12 from collections import defaultdict
---> 14 import numpy as np
     16 from . import __version__
     17 from ._config import config_context, get_config

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__init__.py:135
    131 except ImportError as e:
    132     msg = """Error importing numpy: you should not try to import numpy from
    133     its source directory; please exit the numpy source tree, and relaunch
    134     your python interpreter from there."""
--> 135     raise ImportError(msg) from e
    137 __all__ = [
    138     'exceptions', 'ModuleDeprecationWarning', 'VisibleDeprecationWarning',
    139     'ComplexWarning', 'TooHardError', 'AxisError']
    141 # mapping of {name: (value, deprecation_msg)}

ImportError: Error importing numpy: you should not try to import numpy from
        its source directory; please exit the numpy source tree, and relaunch
        your python interpreter from there.

Hier zeigt sich, dass der Entscheidungsbaum den Ein/Aus-Zustand perfekt vorhersagen kann. Die Logistischen Regressionsmodelle im Vergleich erreichten nur eine Genauigkeit von 54% und 60%.

Es ist zu beachten, dass Modelle mit dieser perfekten Qualität meist nicht gewollt sind, da sie Überfitten (Overfitting) und dann nicht gut generalisieren. Generalisierung bedeutet, dass das Modell auch gut anwendbar auf neue Datensätze ist.

Overfitting, Train-Test-Split und Kreuzvalidation

Um das Überfitting besser zu erkennen und die Generalisierbarkeit eines Modelles zu bewerten, verwendet man üblicherweise zur Bewertung und zum Vergleich von Modellen nicht einfach den Trainingsdatensatz, sondern teilt die Daten in einen Datensatz zum Trainieren und einem zum Testen (Train-Test-Split). Dabei darf der Testdatensatz keine Trainingsdaten enthalten.

Teilen wir den Datensatz einmal in einen Test- und einen Trainingsdatensatz mit jeweils 60% und 40% Daten auf und trainieren das Modell nur auf dem Trainingsdatensatz.

egywth_train=egywth.head(int(egywth.shape[0]*6/10)).copy()
egywth_test=egywth.tail(int(egywth.shape[0]*4/10)).copy()

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[18], line 1
----> 1 egywth_train=egywth.head(int(egywth.shape[0]*6/10)).copy()
      2 egywth_test=egywth.tail(int(egywth.shape[0]*4/10)).copy()

NameError: name 'egywth' is not defined

clfHT_T = DecisionTreeClassifier()
clfHT_T.fit(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]], egywth_train[['EV_HT_740_IS_ON']])
clfHT_T.get_depth()

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[19], line 1
----> 1 clfHT_T = DecisionTreeClassifier()
      2 clfHT_T.fit(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]], egywth_train[['EV_HT_740_IS_ON']])
      3 clfHT_T.get_depth()

NameError: name 'DecisionTreeClassifier' is not defined

egywth_train["pred_DT"] = clfHT_T.predict(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]])
print('Train Accuracy: {:.2f}'.format(accuracy_score(egywth_train.EV_HT_740_IS_ON.values, egywth_train.pred_DT)))

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[20], line 1
----> 1 egywth_train["pred_DT"] = clfHT_T.predict(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]])
      2 print('Train Accuracy: {:.2f}'.format(accuracy_score(egywth_train.EV_HT_740_IS_ON.values, egywth_train.pred_DT)))

NameError: name 'clfHT_T' is not defined

Wir erhalten wieder ein Modell, das zu 100% korrekt vorhersagt.

Wenden wir das Modell einmal auf dem Testdatensatz an.

egywth_test["pred_DT"] = clfHT_T.predict(egywth_test[["SDK", "NM", "VPM", "TMK", "Weekday"]])
print('Test Accuracy: {:.2f}'.format(accuracy_score(egywth_test.EV_HT_740_IS_ON.values, egywth_test.pred_DT)))

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[21], line 1
----> 1 egywth_test["pred_DT"] = clfHT_T.predict(egywth_test[["SDK", "NM", "VPM", "TMK", "Weekday"]])
      2 print('Test Accuracy: {:.2f}'.format(accuracy_score(egywth_test.EV_HT_740_IS_ON.values, egywth_test.pred_DT)))

NameError: name 'clfHT_T' is not defined

Wir sehen jetzt, dass das Modell auf einmal sehr schlecht ist mit einer Genauigkeit von nur 16% (wir bedenken, dass eine Zufallswahl bereits 50% Genauigkeit hat). Das Modell, das also im Training perfekt war, ist im Test komplett schlecht. Das liegt zum einen daran, dass wir in der Logistischen Regression bereits gesehen haben, dass der Energieverbrauch im hinteren Bereich nahezu immer aktiv ist, also der Testdatensatz nicht dem Trainingsdatensatz gut entspricht. Dadurch lernt das Modell ein Verhalten, das im Testdatensatz gar nicht mehr vorkommt.

Dies können wir verhindern, indem wir die Trainings und Testdaten zufällig auswählen.

from sklearn.model_selection import train_test_split

egywthN=egywth.dropna()  # Wir entfernen hier wieder die NaN Werte, da einige Ensemble-Methoden keine NaN Werte unterstützen
egywth_train, egywth_test = train_test_split(egywthN, test_size=0.4)

---------------------------------------------------------------------------
ImportError                               Traceback (most recent call last)
File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/__init__.py:24
     23 try:
---> 24     from . import multiarray
     25 except ImportError as exc:

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/multiarray.py:10
      9 import functools
---> 10 from . import overrides
     11 from . import _multiarray_umath

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/overrides.py:8
      7 from .._utils._inspect import getargspec
----> 8 from numpy.core._multiarray_umath import (
      9     add_docstring,  _get_implementing_args, _ArrayFunctionDispatcher)
     12 ARRAY_FUNCTIONS = set()

ImportError: dlopen(/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/_multiarray_umath.cpython-311-darwin.so, 0x0002): Library not loaded: @rpath/libgfortran.5.dylib
  Referenced from: <342C6FCD-A261-33D7-B978-626161CFD49B> /opt/miniconda3/envs/lehre/lib/libopenblas.0.dylib
  Reason: tried: '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/usr/local/lib/libgfortran.5.dylib' (no such file), '/usr/lib/libgfortran.5.dylib' (no such file, not in dyld cache)

During handling of the above exception, another exception occurred:

ImportError                               Traceback (most recent call last)
File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__init__.py:130
    129 try:
--> 130     from numpy.__config__ import show as show_config
    131 except ImportError as e:

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__config__.py:4
      3 from enum import Enum
----> 4 from numpy.core._multiarray_umath import (
      5     __cpu_features__,
      6     __cpu_baseline__,
      7     __cpu_dispatch__,
      8 )
     10 __all__ = ["show"]

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/__init__.py:50
     27     msg = """
     28 
     29 IMPORTANT: PLEASE READ THIS FOR ADVICE ON HOW TO SOLVE THIS ISSUE!
   (...)
     48 """ % (sys.version_info[0], sys.version_info[1], sys.executable,
     49         __version__, exc)
---> 50     raise ImportError(msg)
     51 finally:

ImportError: 

IMPORTANT: PLEASE READ THIS FOR ADVICE ON HOW TO SOLVE THIS ISSUE!

Importing the numpy C-extensions failed. This error can happen for
many reasons, often due to issues with your setup or how NumPy was
installed.

We have compiled some common reasons and troubleshooting tips at:

    https://numpy.org/devdocs/user/troubleshooting-importerror.html

Please note and check the following:

  * The Python version is: Python3.11 from "/opt/miniconda3/envs/lehre/bin/python"
  * The NumPy version is: "1.26.4"

and make sure that they are the versions you expect.
Please carefully study the documentation linked above for further help.

Original error was: dlopen(/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/_multiarray_umath.cpython-311-darwin.so, 0x0002): Library not loaded: @rpath/libgfortran.5.dylib
  Referenced from: <342C6FCD-A261-33D7-B978-626161CFD49B> /opt/miniconda3/envs/lehre/lib/libopenblas.0.dylib
  Reason: tried: '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/usr/local/lib/libgfortran.5.dylib' (no such file), '/usr/lib/libgfortran.5.dylib' (no such file, not in dyld cache)


The above exception was the direct cause of the following exception:

ImportError                               Traceback (most recent call last)
Cell In[22], line 1
----> 1 from sklearn.model_selection import train_test_split
      3 egywthN=egywth.dropna()  # Wir entfernen hier wieder die NaN Werte, da einige Ensemble-Methoden keine NaN Werte unterstützen
      4 egywth_train, egywth_test = train_test_split(egywthN, test_size=0.4)

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/sklearn/__init__.py:73
     62 # `_distributor_init` allows distributors to run custom init code.
     63 # For instance, for the Windows wheel, this is used to pre-load the
     64 # vcomp shared library runtime for OpenMP embedded in the sklearn/.libs
   (...)
     67 # later is linked to the OpenMP runtime to make it possible to introspect
     68 # it and importing it first would fail if the OpenMP dll cannot be found.
     69 from . import (  # noqa: F401 E402
     70     __check_build,
     71     _distributor_init,
     72 )
---> 73 from .base import clone  # noqa: E402
     74 from .utils._show_versions import show_versions  # noqa: E402
     76 _submodules = [
     77     "calibration",
     78     "cluster",
   (...)
    114     "compose",
    115 ]

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/sklearn/base.py:14
     11 import warnings
     12 from collections import defaultdict
---> 14 import numpy as np
     16 from . import __version__
     17 from ._config import config_context, get_config

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__init__.py:135
    131 except ImportError as e:
    132     msg = """Error importing numpy: you should not try to import numpy from
    133     its source directory; please exit the numpy source tree, and relaunch
    134     your python interpreter from there."""
--> 135     raise ImportError(msg) from e
    137 __all__ = [
    138     'exceptions', 'ModuleDeprecationWarning', 'VisibleDeprecationWarning',
    139     'ComplexWarning', 'TooHardError', 'AxisError']
    141 # mapping of {name: (value, deprecation_msg)}

ImportError: Error importing numpy: you should not try to import numpy from
        its source directory; please exit the numpy source tree, and relaunch
        your python interpreter from there.

clfHT_T = DecisionTreeClassifier()
clfHT_T.fit(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]], egywth_train[['EV_HT_740_IS_ON']])
clfHT_T.get_depth()

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[23], line 1
----> 1 clfHT_T = DecisionTreeClassifier()
      2 clfHT_T.fit(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]], egywth_train[['EV_HT_740_IS_ON']])
      3 clfHT_T.get_depth()

NameError: name 'DecisionTreeClassifier' is not defined

egywth_train["pred_DT"] = clfHT_T.predict(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]])
print('Train Accuracy: {:.2f}'.format(accuracy_score(egywth_train.EV_HT_740_IS_ON.values, egywth_train.pred_DT)))

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[24], line 1
----> 1 egywth_train["pred_DT"] = clfHT_T.predict(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]])
      2 print('Train Accuracy: {:.2f}'.format(accuracy_score(egywth_train.EV_HT_740_IS_ON.values, egywth_train.pred_DT)))

NameError: name 'clfHT_T' is not defined

egywth_test["pred_DT"] = clfHT_T.predict(egywth_test[["SDK", "NM", "VPM", "TMK", "Weekday"]])
print('Test Accuracy: {:.2f}'.format(accuracy_score(egywth_test.EV_HT_740_IS_ON.values, egywth_test.pred_DT)))

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[25], line 1
----> 1 egywth_test["pred_DT"] = clfHT_T.predict(egywth_test[["SDK", "NM", "VPM", "TMK", "Weekday"]])
      2 print('Test Accuracy: {:.2f}'.format(accuracy_score(egywth_test.EV_HT_740_IS_ON.values, egywth_test.pred_DT)))

NameError: name 'clfHT_T' is not defined

Um Abzusichern, dass man nicht zufällig ein guter Test- und Trainingsdatensatz auswählt, empfiehlt es sich das Sampling und Training mehrmals hintereinander zu wiederholen. Diese Verfahren nennt man \(k\)-Kreuzvalidation (\(k\)-Cross-Validation) wobei \(k\) die Anzahl der Wiederholungen ist. Auch hierfür bietet sklearn eine vorhandene Unterstützungsfunktion an.

from sklearn.model_selection import cross_val_score

cross_val_score(clfHT_T, egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]], egywth_train[['EV_HT_740_IS_ON']], cv=5)

---------------------------------------------------------------------------
ImportError                               Traceback (most recent call last)
File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/__init__.py:24
     23 try:
---> 24     from . import multiarray
     25 except ImportError as exc:

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/multiarray.py:10
      9 import functools
---> 10 from . import overrides
     11 from . import _multiarray_umath

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/overrides.py:8
      7 from .._utils._inspect import getargspec
----> 8 from numpy.core._multiarray_umath import (
      9     add_docstring,  _get_implementing_args, _ArrayFunctionDispatcher)
     12 ARRAY_FUNCTIONS = set()

ImportError: dlopen(/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/_multiarray_umath.cpython-311-darwin.so, 0x0002): Library not loaded: @rpath/libgfortran.5.dylib
  Referenced from: <342C6FCD-A261-33D7-B978-626161CFD49B> /opt/miniconda3/envs/lehre/lib/libopenblas.0.dylib
  Reason: tried: '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/usr/local/lib/libgfortran.5.dylib' (no such file), '/usr/lib/libgfortran.5.dylib' (no such file, not in dyld cache)

During handling of the above exception, another exception occurred:

ImportError                               Traceback (most recent call last)
File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__init__.py:130
    129 try:
--> 130     from numpy.__config__ import show as show_config
    131 except ImportError as e:

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__config__.py:4
      3 from enum import Enum
----> 4 from numpy.core._multiarray_umath import (
      5     __cpu_features__,
      6     __cpu_baseline__,
      7     __cpu_dispatch__,
      8 )
     10 __all__ = ["show"]

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/__init__.py:50
     27     msg = """
     28 
     29 IMPORTANT: PLEASE READ THIS FOR ADVICE ON HOW TO SOLVE THIS ISSUE!
   (...)
     48 """ % (sys.version_info[0], sys.version_info[1], sys.executable,
     49         __version__, exc)
---> 50     raise ImportError(msg)
     51 finally:

ImportError: 

IMPORTANT: PLEASE READ THIS FOR ADVICE ON HOW TO SOLVE THIS ISSUE!

Importing the numpy C-extensions failed. This error can happen for
many reasons, often due to issues with your setup or how NumPy was
installed.

We have compiled some common reasons and troubleshooting tips at:

    https://numpy.org/devdocs/user/troubleshooting-importerror.html

Please note and check the following:

  * The Python version is: Python3.11 from "/opt/miniconda3/envs/lehre/bin/python"
  * The NumPy version is: "1.26.4"

and make sure that they are the versions you expect.
Please carefully study the documentation linked above for further help.

Original error was: dlopen(/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/_multiarray_umath.cpython-311-darwin.so, 0x0002): Library not loaded: @rpath/libgfortran.5.dylib
  Referenced from: <342C6FCD-A261-33D7-B978-626161CFD49B> /opt/miniconda3/envs/lehre/lib/libopenblas.0.dylib
  Reason: tried: '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/usr/local/lib/libgfortran.5.dylib' (no such file), '/usr/lib/libgfortran.5.dylib' (no such file, not in dyld cache)


The above exception was the direct cause of the following exception:

ImportError                               Traceback (most recent call last)
Cell In[26], line 1
----> 1 from sklearn.model_selection import cross_val_score
      3 cross_val_score(clfHT_T, egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]], egywth_train[['EV_HT_740_IS_ON']], cv=5)

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/sklearn/__init__.py:73
     62 # `_distributor_init` allows distributors to run custom init code.
     63 # For instance, for the Windows wheel, this is used to pre-load the
     64 # vcomp shared library runtime for OpenMP embedded in the sklearn/.libs
   (...)
     67 # later is linked to the OpenMP runtime to make it possible to introspect
     68 # it and importing it first would fail if the OpenMP dll cannot be found.
     69 from . import (  # noqa: F401 E402
     70     __check_build,
     71     _distributor_init,
     72 )
---> 73 from .base import clone  # noqa: E402
     74 from .utils._show_versions import show_versions  # noqa: E402
     76 _submodules = [
     77     "calibration",
     78     "cluster",
   (...)
    114     "compose",
    115 ]

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/sklearn/base.py:14
     11 import warnings
     12 from collections import defaultdict
---> 14 import numpy as np
     16 from . import __version__
     17 from ._config import config_context, get_config

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__init__.py:135
    131 except ImportError as e:
    132     msg = """Error importing numpy: you should not try to import numpy from
    133     its source directory; please exit the numpy source tree, and relaunch
    134     your python interpreter from there."""
--> 135     raise ImportError(msg) from e
    137 __all__ = [
    138     'exceptions', 'ModuleDeprecationWarning', 'VisibleDeprecationWarning',
    139     'ComplexWarning', 'TooHardError', 'AxisError']
    141 # mapping of {name: (value, deprecation_msg)}

ImportError: Error importing numpy: you should not try to import numpy from
        its source directory; please exit the numpy source tree, and relaunch
        your python interpreter from there.

Hier sehen, wir das trotz der Zufallsauswahl das für die Trainingsdaten ideale Modell immer noch nicht gut die Testdaten vorhersagen kann, es also nicht nur daran liegt, das nicht genug Daten verfügbar sind, sondern, das overfitted Modell einfach sich relativ schlecht generalisieren lässt. Das ist eine typische Eigenschaft von Entscheidungsbäumen.

Das Problem lässt sich reduzieren, wenn man die Tiefe der Bäume reduziert.

clfHT_T2 = DecisionTreeClassifier(max_depth=10)
clfHT_T2.fit(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]], egywth_train[['EV_HT_740_IS_ON']])
clfHT_T2.get_depth()

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[27], line 1
----> 1 clfHT_T2 = DecisionTreeClassifier(max_depth=10)
      2 clfHT_T2.fit(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]], egywth_train[['EV_HT_740_IS_ON']])
      3 clfHT_T2.get_depth()

NameError: name 'DecisionTreeClassifier' is not defined

egywth_train["pred_DT2"] = clfHT_T2.predict(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]])
print('Train Accuracy: {:.2f}'.format(accuracy_score(egywth_train.EV_HT_740_IS_ON.values, egywth_train.pred_DT2)))

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[28], line 1
----> 1 egywth_train["pred_DT2"] = clfHT_T2.predict(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]])
      2 print('Train Accuracy: {:.2f}'.format(accuracy_score(egywth_train.EV_HT_740_IS_ON.values, egywth_train.pred_DT2)))

NameError: name 'clfHT_T2' is not defined

egywth_test["pred_DT2"] = clfHT_T2.predict(egywth_test[["SDK", "NM", "VPM", "TMK", "Weekday"]])
print('Test Accuracy: {:.2f}'.format(accuracy_score(egywth_test.EV_HT_740_IS_ON.values, egywth_test.pred_DT2)))

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[29], line 1
----> 1 egywth_test["pred_DT2"] = clfHT_T2.predict(egywth_test[["SDK", "NM", "VPM", "TMK", "Weekday"]])
      2 print('Test Accuracy: {:.2f}'.format(accuracy_score(egywth_test.EV_HT_740_IS_ON.values, egywth_test.pred_DT2)))

NameError: name 'clfHT_T2' is not defined

Dadurch wird zwar die Qualität des Modells auf dem Trainingsdatensatz schlechter, aber überraschenderweise steigt meist die Qualität auf dem Testdatensatz.

Kombinationsmodelle (Ensemble Models)

Wir haben am obigen Beispiel gesehen, dass Entscheidungsbäume stark zu Overfitting neigen. Deshalb hat man verschiedene Modellvarianten entwickelt, welche die Generalisierbarkeit und somit Gesamtgenauigkeit verbessern, aber die Vorteile des einfachen Modellkonzeptes beibehalten.

Diese Modellvarianten nutzen die Idee mehrere einfache Modelle zu kombinieren. Sie werden als Ensemble-Modells bezeichnet. Das Hauptziel von Ensemble-Modellen ist es, die Vorhersagegenauigkeit zu erhöhen und die Schwächen einzelner Modelle zu kompensieren (wie Overfitting), da durch die Kombination mehrerer Modelle tendenziell die Varianz reduziert wird. Der Nachteil von Ensemble-Modellen ist der erhöhte Rechenbedarfs. Insbesondere beim Stacking und Voting werden vollständige Modelle trainiert, wodurch der Rechenaufwand steigt.

Es gibt verschiedene Ansätze zur Erstellung von Ensemble-Modellen, die sich in der Art und Weise unterscheiden, wie die einzelnen Modelle kombiniert werden:

• Bagging (Bootstrap Aggregation): Mehrere Modelle werden unabhängig voneinander auf verschiedenen Stichproben des Trainingsdatensatzes trainiert, die durch Ziehen mit Zurücklegen (Bootstrap-Sampling) erzeugt werden.

• Boosting: Modelle werden sequenziell trainiert, wobei jedes neue Modell darauf abzielt, die Fehler der vorherigen Modelle zu korrigieren. Jedes Modell wird somit fokussierter und trägt dazu bei, die Gesamtleistung zu verbessern.

• Stacking: Mehrere Modelle unterschiedlichen Typs (Basislerner) werden parallel trainiert um ihre Stärken zu kombinieren. Dieses Metamodell lernt, die Vorhersagen der Basislerner zu kombinieren, um eine endgültige Vorhersage zu treffen.

• Voting: Die Vorhersagen mehrerer Modelle werden kombiniert, indem über die Vorhersagen abgestimmt wird. Für Klassifikationsprobleme kann dies Mehrheitsabstimmung (die Klasse mit den meisten Stimmen wird ausgewählt) sein, während für Regressionsprobleme eine Mittelung der Vorhersagen vorgenommen werden kann.

Bagging/Bootstrap - Random Forest

Random Forests ist eine der beliebtesten Ensemble-Modelle. Es ist eine Bagging-Variante eines Entscheidungsbaumes, bei dem mehrere kleinere Bäume auf zufällige Ausschnitte des Datensatzes trainiert, dadurch soll das Overfitting vermieden werden und somit die Genauigkeit bei der Generalisierung verbessert werden. Wir können uns prinzipiell einen Random Forest selbst aus einzelnen Entscheidungsbäumen erstellen.

forest=[]
for i in range(50):
    egywth_train_sub=egywth_train.sample(int(0.2*egywth_train.shape[0]))
    tree = DecisionTreeClassifier(max_depth=4)
    tree.fit(egywth_train_sub[["SDK", "NM", "VPM", "TMK", "Weekday"]], egywth_train_sub.EV_HT_740_IS_ON.values)
    forest.append(tree)

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[30], line 3
      1 forest=[]
      2 for i in range(50):
----> 3     egywth_train_sub=egywth_train.sample(int(0.2*egywth_train.shape[0]))
      4     tree = DecisionTreeClassifier(max_depth=4)
      5     tree.fit(egywth_train_sub[["SDK", "NM", "VPM", "TMK", "Weekday"]], egywth_train_sub.EV_HT_740_IS_ON.values)

NameError: name 'egywth_train' is not defined

Wir sehen, dass die einzelnen Bäume kleiner sind, da sie einzeln weniger Fälle modellieren müssen.

Zur Vorhersage berechnen wir das Mehrheitsvotum der Vorhersage aller Bäume bei diskreten Daten und den Mittelwert der Vorhersage der einzelnen Bäume bei numerischen Daten bei Regressionsmodellen.

pred=np.zeros(egywth_train.shape[0])
for tree in forest:
    pred += tree.predict(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]]).astype(int)
egywth_train['pred_forest']= pred > len(forest)/2 # da dies eine binäre vorhersage ist berechnen wir den Mehreitsvote

print('Train Accuracy: {:.2f}'.format(accuracy_score(egywth_train.EV_HT_740_IS_ON.values, egywth_train.pred_forest)))

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[31], line 1
----> 1 pred=np.zeros(egywth_train.shape[0])
      2 for tree in forest:
      3     pred += tree.predict(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]]).astype(int)

NameError: name 'np' is not defined

pred=np.zeros(egywth_test.shape[0])
for tree in forest: 
    pred += tree.predict(egywth_test[["SDK", "NM", "VPM", "TMK", "Weekday"]])
egywth_test['pred_forest']= pred > len(forest)/2 # Mehreitsvote

print('Test Accuracy: {:.2f}'.format(accuracy_score(egywth_test.EV_HT_740_IS_ON.values, egywth_test.pred_forest)))

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[32], line 1
----> 1 pred=np.zeros(egywth_test.shape[0])
      2 for tree in forest: 
      3     pred += tree.predict(egywth_test[["SDK", "NM", "VPM", "TMK", "Weekday"]])

NameError: name 'np' is not defined

In der Praxis nutzt man den fertigen Wald aus sklearn.ensemble, welche standartmäßig mit 100 Bäumen arbeitet.

from sklearn.ensemble import RandomForestClassifier
clf_RF = RandomForestClassifier()
clf_RF.fit(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]], egywth_train.EV_HT_740_IS_ON.values)

---------------------------------------------------------------------------
ImportError                               Traceback (most recent call last)
File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/__init__.py:24
     23 try:
---> 24     from . import multiarray
     25 except ImportError as exc:

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/multiarray.py:10
      9 import functools
---> 10 from . import overrides
     11 from . import _multiarray_umath

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/overrides.py:8
      7 from .._utils._inspect import getargspec
----> 8 from numpy.core._multiarray_umath import (
      9     add_docstring,  _get_implementing_args, _ArrayFunctionDispatcher)
     12 ARRAY_FUNCTIONS = set()

ImportError: dlopen(/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/_multiarray_umath.cpython-311-darwin.so, 0x0002): Library not loaded: @rpath/libgfortran.5.dylib
  Referenced from: <342C6FCD-A261-33D7-B978-626161CFD49B> /opt/miniconda3/envs/lehre/lib/libopenblas.0.dylib
  Reason: tried: '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/usr/local/lib/libgfortran.5.dylib' (no such file), '/usr/lib/libgfortran.5.dylib' (no such file, not in dyld cache)

During handling of the above exception, another exception occurred:

ImportError                               Traceback (most recent call last)
File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__init__.py:130
    129 try:
--> 130     from numpy.__config__ import show as show_config
    131 except ImportError as e:

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__config__.py:4
      3 from enum import Enum
----> 4 from numpy.core._multiarray_umath import (
      5     __cpu_features__,
      6     __cpu_baseline__,
      7     __cpu_dispatch__,
      8 )
     10 __all__ = ["show"]

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/__init__.py:50
     27     msg = """
     28 
     29 IMPORTANT: PLEASE READ THIS FOR ADVICE ON HOW TO SOLVE THIS ISSUE!
   (...)
     48 """ % (sys.version_info[0], sys.version_info[1], sys.executable,
     49         __version__, exc)
---> 50     raise ImportError(msg)
     51 finally:

ImportError: 

IMPORTANT: PLEASE READ THIS FOR ADVICE ON HOW TO SOLVE THIS ISSUE!

Importing the numpy C-extensions failed. This error can happen for
many reasons, often due to issues with your setup or how NumPy was
installed.

We have compiled some common reasons and troubleshooting tips at:

    https://numpy.org/devdocs/user/troubleshooting-importerror.html

Please note and check the following:

  * The Python version is: Python3.11 from "/opt/miniconda3/envs/lehre/bin/python"
  * The NumPy version is: "1.26.4"

and make sure that they are the versions you expect.
Please carefully study the documentation linked above for further help.

Original error was: dlopen(/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/_multiarray_umath.cpython-311-darwin.so, 0x0002): Library not loaded: @rpath/libgfortran.5.dylib
  Referenced from: <342C6FCD-A261-33D7-B978-626161CFD49B> /opt/miniconda3/envs/lehre/lib/libopenblas.0.dylib
  Reason: tried: '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/usr/local/lib/libgfortran.5.dylib' (no such file), '/usr/lib/libgfortran.5.dylib' (no such file, not in dyld cache)


The above exception was the direct cause of the following exception:

ImportError                               Traceback (most recent call last)
Cell In[33], line 1
----> 1 from sklearn.ensemble import RandomForestClassifier
      2 clf_RF = RandomForestClassifier()
      3 clf_RF.fit(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]], egywth_train.EV_HT_740_IS_ON.values)

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/sklearn/__init__.py:73
     62 # `_distributor_init` allows distributors to run custom init code.
     63 # For instance, for the Windows wheel, this is used to pre-load the
     64 # vcomp shared library runtime for OpenMP embedded in the sklearn/.libs
   (...)
     67 # later is linked to the OpenMP runtime to make it possible to introspect
     68 # it and importing it first would fail if the OpenMP dll cannot be found.
     69 from . import (  # noqa: F401 E402
     70     __check_build,
     71     _distributor_init,
     72 )
---> 73 from .base import clone  # noqa: E402
     74 from .utils._show_versions import show_versions  # noqa: E402
     76 _submodules = [
     77     "calibration",
     78     "cluster",
   (...)
    114     "compose",
    115 ]

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/sklearn/base.py:14
     11 import warnings
     12 from collections import defaultdict
---> 14 import numpy as np
     16 from . import __version__
     17 from ._config import config_context, get_config

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__init__.py:135
    131 except ImportError as e:
    132     msg = """Error importing numpy: you should not try to import numpy from
    133     its source directory; please exit the numpy source tree, and relaunch
    134     your python interpreter from there."""
--> 135     raise ImportError(msg) from e
    137 __all__ = [
    138     'exceptions', 'ModuleDeprecationWarning', 'VisibleDeprecationWarning',
    139     'ComplexWarning', 'TooHardError', 'AxisError']
    141 # mapping of {name: (value, deprecation_msg)}

ImportError: Error importing numpy: you should not try to import numpy from
        its source directory; please exit the numpy source tree, and relaunch
        your python interpreter from there.

Mit der bekannten Predict Methode.

egywth_train["pred_RF"] = clf_RF.predict(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]])
print('Train Accuracy: {:.2f}'.format(accuracy_score(egywth_train.EV_HT_740_IS_ON.values, egywth_train.pred_RF)))

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[34], line 1
----> 1 egywth_train["pred_RF"] = clf_RF.predict(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]])
      2 print('Train Accuracy: {:.2f}'.format(accuracy_score(egywth_train.EV_HT_740_IS_ON.values, egywth_train.pred_RF)))

NameError: name 'clf_RF' is not defined

egywth_test["pred_RF"] = clf_RF.predict(egywth_test[["SDK", "NM", "VPM", "TMK", "Weekday"]])
print('Test Accuracy: {:.2f}'.format(accuracy_score(egywth_test.EV_HT_740_IS_ON.values, egywth_test.pred_RF)))

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[35], line 1
----> 1 egywth_test["pred_RF"] = clf_RF.predict(egywth_test[["SDK", "NM", "VPM", "TMK", "Weekday"]])
      2 print('Test Accuracy: {:.2f}'.format(accuracy_score(egywth_test.EV_HT_740_IS_ON.values, egywth_test.pred_RF)))

NameError: name 'clf_RF' is not defined

Das Ergebnis ist schon besser als der einfache Entscheidungsbaum.

Boosting

Boosting ist eine andere Methode zum Erstellen von Ensemble-Modellen, bei der eine Reihe schwacher Modelle (d. h. Modelle, die nur geringfügig besser als Zufallsvorhersagen sind) sequenziell trainiert und kombiniert werden, um ein starkes Modell zu erstellen. Die Grundidee besteht darin, aufeinanderfolgende Modelle so zu trainieren, dass sie die Fehler der vorhergehenden Modelle korrigieren.

Aber Achtung: Da Boosting-Algorithmen stark auf schwerwiegende Fehler fokussieren, können sie empfindlich gegenüber Ausreißern sein.

Adaboost

AdaBoost ist eines der bekanntesten boosting Modelle. Es beginnt mit einem schwachen Modell, das auf den gesamten Datensatz trainiert wird. In den folgenden Iterationen werden die Gewichte der falsch klassifizierten Datenpunkte erhöht und ein neues Modell wird trainiert. Dies wiederholt sich, und die Modelle werden so kombiniert, dass sie schwerwiegendere Fehler korrigieren. AdaBoost ist einfach zu implementieren und funktioniert gut mit vielen Basislernern, wie Entscheidungsstümpfen (einfachen Entscheidungsbäumen).

from sklearn.ensemble import AdaBoostClassifier
clf_AB = AdaBoostClassifier()
clf_AB.fit(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]], egywth_train.EV_HT_740_IS_ON.values)

---------------------------------------------------------------------------
ImportError                               Traceback (most recent call last)
File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/__init__.py:24
     23 try:
---> 24     from . import multiarray
     25 except ImportError as exc:

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/multiarray.py:10
      9 import functools
---> 10 from . import overrides
     11 from . import _multiarray_umath

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/overrides.py:8
      7 from .._utils._inspect import getargspec
----> 8 from numpy.core._multiarray_umath import (
      9     add_docstring,  _get_implementing_args, _ArrayFunctionDispatcher)
     12 ARRAY_FUNCTIONS = set()

ImportError: dlopen(/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/_multiarray_umath.cpython-311-darwin.so, 0x0002): Library not loaded: @rpath/libgfortran.5.dylib
  Referenced from: <342C6FCD-A261-33D7-B978-626161CFD49B> /opt/miniconda3/envs/lehre/lib/libopenblas.0.dylib
  Reason: tried: '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/usr/local/lib/libgfortran.5.dylib' (no such file), '/usr/lib/libgfortran.5.dylib' (no such file, not in dyld cache)

During handling of the above exception, another exception occurred:

ImportError                               Traceback (most recent call last)
File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__init__.py:130
    129 try:
--> 130     from numpy.__config__ import show as show_config
    131 except ImportError as e:

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__config__.py:4
      3 from enum import Enum
----> 4 from numpy.core._multiarray_umath import (
      5     __cpu_features__,
      6     __cpu_baseline__,
      7     __cpu_dispatch__,
      8 )
     10 __all__ = ["show"]

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/__init__.py:50
     27     msg = """
     28 
     29 IMPORTANT: PLEASE READ THIS FOR ADVICE ON HOW TO SOLVE THIS ISSUE!
   (...)
     48 """ % (sys.version_info[0], sys.version_info[1], sys.executable,
     49         __version__, exc)
---> 50     raise ImportError(msg)
     51 finally:

ImportError: 

IMPORTANT: PLEASE READ THIS FOR ADVICE ON HOW TO SOLVE THIS ISSUE!

Importing the numpy C-extensions failed. This error can happen for
many reasons, often due to issues with your setup or how NumPy was
installed.

We have compiled some common reasons and troubleshooting tips at:

    https://numpy.org/devdocs/user/troubleshooting-importerror.html

Please note and check the following:

  * The Python version is: Python3.11 from "/opt/miniconda3/envs/lehre/bin/python"
  * The NumPy version is: "1.26.4"

and make sure that they are the versions you expect.
Please carefully study the documentation linked above for further help.

Original error was: dlopen(/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/_multiarray_umath.cpython-311-darwin.so, 0x0002): Library not loaded: @rpath/libgfortran.5.dylib
  Referenced from: <342C6FCD-A261-33D7-B978-626161CFD49B> /opt/miniconda3/envs/lehre/lib/libopenblas.0.dylib
  Reason: tried: '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/usr/local/lib/libgfortran.5.dylib' (no such file), '/usr/lib/libgfortran.5.dylib' (no such file, not in dyld cache)


The above exception was the direct cause of the following exception:

ImportError                               Traceback (most recent call last)
Cell In[36], line 1
----> 1 from sklearn.ensemble import AdaBoostClassifier
      2 clf_AB = AdaBoostClassifier()
      3 clf_AB.fit(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]], egywth_train.EV_HT_740_IS_ON.values)

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/sklearn/__init__.py:73
     62 # `_distributor_init` allows distributors to run custom init code.
     63 # For instance, for the Windows wheel, this is used to pre-load the
     64 # vcomp shared library runtime for OpenMP embedded in the sklearn/.libs
   (...)
     67 # later is linked to the OpenMP runtime to make it possible to introspect
     68 # it and importing it first would fail if the OpenMP dll cannot be found.
     69 from . import (  # noqa: F401 E402
     70     __check_build,
     71     _distributor_init,
     72 )
---> 73 from .base import clone  # noqa: E402
     74 from .utils._show_versions import show_versions  # noqa: E402
     76 _submodules = [
     77     "calibration",
     78     "cluster",
   (...)
    114     "compose",
    115 ]

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/sklearn/base.py:14
     11 import warnings
     12 from collections import defaultdict
---> 14 import numpy as np
     16 from . import __version__
     17 from ._config import config_context, get_config

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__init__.py:135
    131 except ImportError as e:
    132     msg = """Error importing numpy: you should not try to import numpy from
    133     its source directory; please exit the numpy source tree, and relaunch
    134     your python interpreter from there."""
--> 135     raise ImportError(msg) from e
    137 __all__ = [
    138     'exceptions', 'ModuleDeprecationWarning', 'VisibleDeprecationWarning',
    139     'ComplexWarning', 'TooHardError', 'AxisError']
    141 # mapping of {name: (value, deprecation_msg)}

ImportError: Error importing numpy: you should not try to import numpy from
        its source directory; please exit the numpy source tree, and relaunch
        your python interpreter from there.

egywth_train["pred_AB"] = clf_AB.predict(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]])
print('Train Accuracy: {:.2f}'.format(accuracy_score(egywth_train.EV_HT_740_IS_ON.values, egywth_train.pred_AB)))

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[37], line 1
----> 1 egywth_train["pred_AB"] = clf_AB.predict(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]])
      2 print('Train Accuracy: {:.2f}'.format(accuracy_score(egywth_train.EV_HT_740_IS_ON.values, egywth_train.pred_AB)))

NameError: name 'clf_AB' is not defined

egywth_test["pred_AB"] = clf_AB.predict(egywth_test[["SDK", "NM", "VPM", "TMK", "Weekday"]])
print('Test Accuracy: {:.2f}'.format(accuracy_score(egywth_test.EV_HT_740_IS_ON.values, egywth_test.pred_AB)))

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[38], line 1
----> 1 egywth_test["pred_AB"] = clf_AB.predict(egywth_test[["SDK", "NM", "VPM", "TMK", "Weekday"]])
      2 print('Test Accuracy: {:.2f}'.format(accuracy_score(egywth_test.EV_HT_740_IS_ON.values, egywth_test.pred_AB)))

NameError: name 'clf_AB' is not defined

Gradient Boosting

Gradient Boosting optimiert ein beliebiges Verlustmaß (z. B. die quadratische Fehlerfunktion bei Regression oder die logarithmische Verlustfunktion bei Klassifikation) durch iteratives Hinzufügen von Modellen, die die negativen Gradienten (Richtungen des steilsten Abstiegs) der Verlustfunktion vorhersagen. Gradient Boosting ist flexibler und leistungsfähiger als AdaBoost, da es eine bessere Optimierung des Verlustmaßes ermöglicht.

from sklearn.ensemble import GradientBoostingClassifier
clf_GB = GradientBoostingClassifier()
clf_GB.fit(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]], egywth_train.EV_HT_740_IS_ON.values)

egywth_train["pred_GB"] = clf_GB.predict(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]])
print('Train Accuracy: {:.2f}'.format(accuracy_score(egywth_train.EV_HT_740_IS_ON.values, egywth_train.pred_GB)))

---------------------------------------------------------------------------
ImportError                               Traceback (most recent call last)
File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/__init__.py:24
     23 try:
---> 24     from . import multiarray
     25 except ImportError as exc:

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/multiarray.py:10
      9 import functools
---> 10 from . import overrides
     11 from . import _multiarray_umath

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/overrides.py:8
      7 from .._utils._inspect import getargspec
----> 8 from numpy.core._multiarray_umath import (
      9     add_docstring,  _get_implementing_args, _ArrayFunctionDispatcher)
     12 ARRAY_FUNCTIONS = set()

ImportError: dlopen(/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/_multiarray_umath.cpython-311-darwin.so, 0x0002): Library not loaded: @rpath/libgfortran.5.dylib
  Referenced from: <342C6FCD-A261-33D7-B978-626161CFD49B> /opt/miniconda3/envs/lehre/lib/libopenblas.0.dylib
  Reason: tried: '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/usr/local/lib/libgfortran.5.dylib' (no such file), '/usr/lib/libgfortran.5.dylib' (no such file, not in dyld cache)

During handling of the above exception, another exception occurred:

ImportError                               Traceback (most recent call last)
File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__init__.py:130
    129 try:
--> 130     from numpy.__config__ import show as show_config
    131 except ImportError as e:

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__config__.py:4
      3 from enum import Enum
----> 4 from numpy.core._multiarray_umath import (
      5     __cpu_features__,
      6     __cpu_baseline__,
      7     __cpu_dispatch__,
      8 )
     10 __all__ = ["show"]

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/__init__.py:50
     27     msg = """
     28 
     29 IMPORTANT: PLEASE READ THIS FOR ADVICE ON HOW TO SOLVE THIS ISSUE!
   (...)
     48 """ % (sys.version_info[0], sys.version_info[1], sys.executable,
     49         __version__, exc)
---> 50     raise ImportError(msg)
     51 finally:

ImportError: 

IMPORTANT: PLEASE READ THIS FOR ADVICE ON HOW TO SOLVE THIS ISSUE!

Importing the numpy C-extensions failed. This error can happen for
many reasons, often due to issues with your setup or how NumPy was
installed.

We have compiled some common reasons and troubleshooting tips at:

    https://numpy.org/devdocs/user/troubleshooting-importerror.html

Please note and check the following:

  * The Python version is: Python3.11 from "/opt/miniconda3/envs/lehre/bin/python"
  * The NumPy version is: "1.26.4"

and make sure that they are the versions you expect.
Please carefully study the documentation linked above for further help.

Original error was: dlopen(/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/_multiarray_umath.cpython-311-darwin.so, 0x0002): Library not loaded: @rpath/libgfortran.5.dylib
  Referenced from: <342C6FCD-A261-33D7-B978-626161CFD49B> /opt/miniconda3/envs/lehre/lib/libopenblas.0.dylib
  Reason: tried: '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/usr/local/lib/libgfortran.5.dylib' (no such file), '/usr/lib/libgfortran.5.dylib' (no such file, not in dyld cache)


The above exception was the direct cause of the following exception:

ImportError                               Traceback (most recent call last)
Cell In[39], line 1
----> 1 from sklearn.ensemble import GradientBoostingClassifier
      2 clf_GB = GradientBoostingClassifier()
      3 clf_GB.fit(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]], egywth_train.EV_HT_740_IS_ON.values)

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/sklearn/__init__.py:73
     62 # `_distributor_init` allows distributors to run custom init code.
     63 # For instance, for the Windows wheel, this is used to pre-load the
     64 # vcomp shared library runtime for OpenMP embedded in the sklearn/.libs
   (...)
     67 # later is linked to the OpenMP runtime to make it possible to introspect
     68 # it and importing it first would fail if the OpenMP dll cannot be found.
     69 from . import (  # noqa: F401 E402
     70     __check_build,
     71     _distributor_init,
     72 )
---> 73 from .base import clone  # noqa: E402
     74 from .utils._show_versions import show_versions  # noqa: E402
     76 _submodules = [
     77     "calibration",
     78     "cluster",
   (...)
    114     "compose",
    115 ]

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/sklearn/base.py:14
     11 import warnings
     12 from collections import defaultdict
---> 14 import numpy as np
     16 from . import __version__
     17 from ._config import config_context, get_config

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__init__.py:135
    131 except ImportError as e:
    132     msg = """Error importing numpy: you should not try to import numpy from
    133     its source directory; please exit the numpy source tree, and relaunch
    134     your python interpreter from there."""
--> 135     raise ImportError(msg) from e
    137 __all__ = [
    138     'exceptions', 'ModuleDeprecationWarning', 'VisibleDeprecationWarning',
    139     'ComplexWarning', 'TooHardError', 'AxisError']
    141 # mapping of {name: (value, deprecation_msg)}

ImportError: Error importing numpy: you should not try to import numpy from
        its source directory; please exit the numpy source tree, and relaunch
        your python interpreter from there.

egywth_test["pred_GB"] = clf_GB.predict(egywth_test[["SDK", "NM", "VPM", "TMK", "Weekday"]])
print('Test Accuracy: {:.2f}'.format(accuracy_score(egywth_test.EV_HT_740_IS_ON.values, egywth_test.pred_GB)))

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[40], line 1
----> 1 egywth_test["pred_GB"] = clf_GB.predict(egywth_test[["SDK", "NM", "VPM", "TMK", "Weekday"]])
      2 print('Test Accuracy: {:.2f}'.format(accuracy_score(egywth_test.EV_HT_740_IS_ON.values, egywth_test.pred_GB)))

NameError: name 'clf_GB' is not defined

XGBoost

XGBoost ist eine erweiterte Version des Gradient Boosting, die auf Effizienz und Geschwindigkeit optimiert ist. Es verwendet Techniken wie Sparsity Awareness, paralleles Tree-Boosting und reguläre Begriffe, um Overfitting zu vermeiden. XGBoost ist sehr beliebt bei großen Datensätzen aufgrund seiner hohen Leistung und Effizienz.

XGBoost ist direkt nicht in sklearn verfügbar. Das xgboost bietet aber die gleiche API an.

import xgboost as xgb

clf_XGB = xgb.XGBClassifier()
clf_XGB.fit(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]], egywth_train.EV_HT_740_IS_ON.values)

---------------------------------------------------------------------------
ImportError                               Traceback (most recent call last)
File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/__init__.py:24
     23 try:
---> 24     from . import multiarray
     25 except ImportError as exc:

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/multiarray.py:10
      9 import functools
---> 10 from . import overrides
     11 from . import _multiarray_umath

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/overrides.py:8
      7 from .._utils._inspect import getargspec
----> 8 from numpy.core._multiarray_umath import (
      9     add_docstring,  _get_implementing_args, _ArrayFunctionDispatcher)
     12 ARRAY_FUNCTIONS = set()

ImportError: dlopen(/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/_multiarray_umath.cpython-311-darwin.so, 0x0002): Library not loaded: @rpath/libgfortran.5.dylib
  Referenced from: <342C6FCD-A261-33D7-B978-626161CFD49B> /opt/miniconda3/envs/lehre/lib/libopenblas.0.dylib
  Reason: tried: '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/usr/local/lib/libgfortran.5.dylib' (no such file), '/usr/lib/libgfortran.5.dylib' (no such file, not in dyld cache)

During handling of the above exception, another exception occurred:

ImportError                               Traceback (most recent call last)
File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__init__.py:130
    129 try:
--> 130     from numpy.__config__ import show as show_config
    131 except ImportError as e:

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__config__.py:4
      3 from enum import Enum
----> 4 from numpy.core._multiarray_umath import (
      5     __cpu_features__,
      6     __cpu_baseline__,
      7     __cpu_dispatch__,
      8 )
     10 __all__ = ["show"]

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/__init__.py:50
     27     msg = """
     28 
     29 IMPORTANT: PLEASE READ THIS FOR ADVICE ON HOW TO SOLVE THIS ISSUE!
   (...)
     48 """ % (sys.version_info[0], sys.version_info[1], sys.executable,
     49         __version__, exc)
---> 50     raise ImportError(msg)
     51 finally:

ImportError: 

IMPORTANT: PLEASE READ THIS FOR ADVICE ON HOW TO SOLVE THIS ISSUE!

Importing the numpy C-extensions failed. This error can happen for
many reasons, often due to issues with your setup or how NumPy was
installed.

We have compiled some common reasons and troubleshooting tips at:

    https://numpy.org/devdocs/user/troubleshooting-importerror.html

Please note and check the following:

  * The Python version is: Python3.11 from "/opt/miniconda3/envs/lehre/bin/python"
  * The NumPy version is: "1.26.4"

and make sure that they are the versions you expect.
Please carefully study the documentation linked above for further help.

Original error was: dlopen(/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/_multiarray_umath.cpython-311-darwin.so, 0x0002): Library not loaded: @rpath/libgfortran.5.dylib
  Referenced from: <342C6FCD-A261-33D7-B978-626161CFD49B> /opt/miniconda3/envs/lehre/lib/libopenblas.0.dylib
  Reason: tried: '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/usr/local/lib/libgfortran.5.dylib' (no such file), '/usr/lib/libgfortran.5.dylib' (no such file, not in dyld cache)


The above exception was the direct cause of the following exception:

ImportError                               Traceback (most recent call last)
Cell In[41], line 1
----> 1 import xgboost as xgb
      3 clf_XGB = xgb.XGBClassifier()
      4 clf_XGB.fit(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]], egywth_train.EV_HT_740_IS_ON.values)

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/xgboost/__init__.py:6
      1 """XGBoost: eXtreme Gradient Boosting library.
      2 
      3 Contributors: https://github.com/dmlc/xgboost/blob/master/CONTRIBUTORS.md
      4 """
----> 6 from . import tracker  # noqa
      7 from . import collective, dask
      8 from .core import (
      9     Booster,
     10     DataIter,
   (...)
     15     build_info,
     16 )

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/xgboost/tracker.py:9
      6 from enum import IntEnum, unique
      7 from typing import Dict, Optional, Union
----> 9 from .core import _LIB, _check_call, make_jcargs
     12 def get_family(addr: str) -> int:
     13     """Get network family from address."""

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/xgboost/core.py:34
     16 from inspect import Parameter, signature
     17 from typing import (
     18     Any,
     19     Callable,
   (...)
     31     overload,
     32 )
---> 34 import numpy as np
     35 import scipy.sparse
     37 from ._typing import (
     38     _T,
     39     ArrayLike,
   (...)
     56     c_bst_ulong,
     57 )

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__init__.py:135
    131 except ImportError as e:
    132     msg = """Error importing numpy: you should not try to import numpy from
    133     its source directory; please exit the numpy source tree, and relaunch
    134     your python interpreter from there."""
--> 135     raise ImportError(msg) from e
    137 __all__ = [
    138     'exceptions', 'ModuleDeprecationWarning', 'VisibleDeprecationWarning',
    139     'ComplexWarning', 'TooHardError', 'AxisError']
    141 # mapping of {name: (value, deprecation_msg)}

ImportError: Error importing numpy: you should not try to import numpy from
        its source directory; please exit the numpy source tree, and relaunch
        your python interpreter from there.

egywth_train["pred_XGB"] = clf_XGB.predict(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]])
print('Train Accuracy: {:.2f}'.format(accuracy_score(egywth_train.EV_HT_740_IS_ON.values, egywth_train.pred_XGB)))

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[42], line 1
----> 1 egywth_train["pred_XGB"] = clf_XGB.predict(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]])
      2 print('Train Accuracy: {:.2f}'.format(accuracy_score(egywth_train.EV_HT_740_IS_ON.values, egywth_train.pred_XGB)))

NameError: name 'clf_XGB' is not defined

egywth_test["pred_XGB"] = clf_XGB.predict(egywth_test[["SDK", "NM", "VPM", "TMK", "Weekday"]])
print('Accuracy: {:.2f}'.format(accuracy_score(egywth_test.EV_HT_740_IS_ON.values, egywth_test.pred_XGB)))

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[43], line 1
----> 1 egywth_test["pred_XGB"] = clf_XGB.predict(egywth_test[["SDK", "NM", "VPM", "TMK", "Weekday"]])
      2 print('Accuracy: {:.2f}'.format(accuracy_score(egywth_test.EV_HT_740_IS_ON.values, egywth_test.pred_XGB)))

NameError: name 'clf_XGB' is not defined

Stacking

Beim Stacking kombiniert man einfach mehrere Modelle durch ein weiteres einfaches Modell. Zum Beispiel wollen wir die Vorhersage des Logistischen Regressionsmodells mit dem Decission Tree kombinieren innerhalb eines weiteren Logistischen Modells kombinieren. Hier können wir insbesondere gut ausnutzen, dass sklearn immer die gleiche API anbietet, wir können also das Training und die Vorhersage einfach als Loop implementieren.

from sklearn.linear_model import LogisticRegression

# 1. Basismodel
clfLR = LogisticRegression()
# 2. Basismodel 
clfDT = DecisionTreeClassifier()
# Stacking
stack=[clfLR, clfDT]

---------------------------------------------------------------------------
ImportError                               Traceback (most recent call last)
File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/__init__.py:24
     23 try:
---> 24     from . import multiarray
     25 except ImportError as exc:

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/multiarray.py:10
      9 import functools
---> 10 from . import overrides
     11 from . import _multiarray_umath

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/overrides.py:8
      7 from .._utils._inspect import getargspec
----> 8 from numpy.core._multiarray_umath import (
      9     add_docstring,  _get_implementing_args, _ArrayFunctionDispatcher)
     12 ARRAY_FUNCTIONS = set()

ImportError: dlopen(/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/_multiarray_umath.cpython-311-darwin.so, 0x0002): Library not loaded: @rpath/libgfortran.5.dylib
  Referenced from: <342C6FCD-A261-33D7-B978-626161CFD49B> /opt/miniconda3/envs/lehre/lib/libopenblas.0.dylib
  Reason: tried: '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/usr/local/lib/libgfortran.5.dylib' (no such file), '/usr/lib/libgfortran.5.dylib' (no such file, not in dyld cache)

During handling of the above exception, another exception occurred:

ImportError                               Traceback (most recent call last)
File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__init__.py:130
    129 try:
--> 130     from numpy.__config__ import show as show_config
    131 except ImportError as e:

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__config__.py:4
      3 from enum import Enum
----> 4 from numpy.core._multiarray_umath import (
      5     __cpu_features__,
      6     __cpu_baseline__,
      7     __cpu_dispatch__,
      8 )
     10 __all__ = ["show"]

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/__init__.py:50
     27     msg = """
     28 
     29 IMPORTANT: PLEASE READ THIS FOR ADVICE ON HOW TO SOLVE THIS ISSUE!
   (...)
     48 """ % (sys.version_info[0], sys.version_info[1], sys.executable,
     49         __version__, exc)
---> 50     raise ImportError(msg)
     51 finally:

ImportError: 

IMPORTANT: PLEASE READ THIS FOR ADVICE ON HOW TO SOLVE THIS ISSUE!

Importing the numpy C-extensions failed. This error can happen for
many reasons, often due to issues with your setup or how NumPy was
installed.

We have compiled some common reasons and troubleshooting tips at:

    https://numpy.org/devdocs/user/troubleshooting-importerror.html

Please note and check the following:

  * The Python version is: Python3.11 from "/opt/miniconda3/envs/lehre/bin/python"
  * The NumPy version is: "1.26.4"

and make sure that they are the versions you expect.
Please carefully study the documentation linked above for further help.

Original error was: dlopen(/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/_multiarray_umath.cpython-311-darwin.so, 0x0002): Library not loaded: @rpath/libgfortran.5.dylib
  Referenced from: <342C6FCD-A261-33D7-B978-626161CFD49B> /opt/miniconda3/envs/lehre/lib/libopenblas.0.dylib
  Reason: tried: '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/usr/local/lib/libgfortran.5.dylib' (no such file), '/usr/lib/libgfortran.5.dylib' (no such file, not in dyld cache)


The above exception was the direct cause of the following exception:

ImportError                               Traceback (most recent call last)
Cell In[44], line 1
----> 1 from sklearn.linear_model import LogisticRegression
      3 # 1. Basismodel
      4 clfLR = LogisticRegression()

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/sklearn/__init__.py:73
     62 # `_distributor_init` allows distributors to run custom init code.
     63 # For instance, for the Windows wheel, this is used to pre-load the
     64 # vcomp shared library runtime for OpenMP embedded in the sklearn/.libs
   (...)
     67 # later is linked to the OpenMP runtime to make it possible to introspect
     68 # it and importing it first would fail if the OpenMP dll cannot be found.
     69 from . import (  # noqa: F401 E402
     70     __check_build,
     71     _distributor_init,
     72 )
---> 73 from .base import clone  # noqa: E402
     74 from .utils._show_versions import show_versions  # noqa: E402
     76 _submodules = [
     77     "calibration",
     78     "cluster",
   (...)
    114     "compose",
    115 ]

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/sklearn/base.py:14
     11 import warnings
     12 from collections import defaultdict
---> 14 import numpy as np
     16 from . import __version__
     17 from ._config import config_context, get_config

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__init__.py:135
    131 except ImportError as e:
    132     msg = """Error importing numpy: you should not try to import numpy from
    133     its source directory; please exit the numpy source tree, and relaunch
    134     your python interpreter from there."""
--> 135     raise ImportError(msg) from e
    137 __all__ = [
    138     'exceptions', 'ModuleDeprecationWarning', 'VisibleDeprecationWarning',
    139     'ComplexWarning', 'TooHardError', 'AxisError']
    141 # mapping of {name: (value, deprecation_msg)}

ImportError: Error importing numpy: you should not try to import numpy from
        its source directory; please exit the numpy source tree, and relaunch
        your python interpreter from there.

Wir trainineren alle Basismodelle

for model in stack:
    model.fit(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]], egywth_train.EV_HT_740_IS_ON.values)

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[45], line 1
----> 1 for model in stack:
      2     model.fit(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]], egywth_train.EV_HT_740_IS_ON.values)

NameError: name 'stack' is not defined

Die Modelle kombinieren wir nun in einem Stackingmodell, was meist ein sehr einfaches logistisches oder lineares Modell ist. Hierfür berechnen wir erst für den Trainingsdatensatz die Vorhersagen und geben die in ein neues gestacktes Modell, das nur die Vorhersagen enthält. Dadurch gewichten wir einfach die Basismodelle in ihrer Güte.

pred_train={}
for i,model in enumerate(stack):
    pred_train[f"pred{i}"]=model.predict(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]])
pred_train=pd.DataFrame(pred_train)

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[46], line 2
      1 pred_train={}
----> 2 for i,model in enumerate(stack):
      3     pred_train[f"pred{i}"]=model.predict(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]])
      4 pred_train=pd.DataFrame(pred_train)

NameError: name 'stack' is not defined

# 4. Stacking Model
clfST = LogisticRegression()
clfST.fit(pred_train, egywth_train.EV_HT_740_IS_ON.values)

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[47], line 2
      1 # 4. Stacking Model
----> 2 clfST = LogisticRegression()
      3 clfST.fit(pred_train, egywth_train.EV_HT_740_IS_ON.values)

NameError: name 'LogisticRegression' is not defined

Bei der Vorhersage machen wir das gleiche und berechnen erst die Vorhersage der Basismodell und kombinieren dann diese in einer Vorhersage durch das Stackingmodell.

pred_test={}
for i,model in enumerate(stack):
    pred_test[f"pred{i}"]=model.predict(egywth_test[["SDK", "NM", "VPM", "TMK", "Weekday"]])
pred_test=pd.DataFrame(pred_test)
egywth_test['pred_stack_lm']= clfST.predict(pred_test)

print('Test Accuracy: {:.2f}'.format(accuracy_score(egywth_test.EV_HT_740_IS_ON.values, egywth_test.pred_stack_lm)))

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[48], line 2
      1 pred_test={}
----> 2 for i,model in enumerate(stack):
      3     pred_test[f"pred{i}"]=model.predict(egywth_test[["SDK", "NM", "VPM", "TMK", "Weekday"]])
      4 pred_test=pd.DataFrame(pred_test)

NameError: name 'stack' is not defined

Auch hierfür bietet sklearn eine einfache Funktion an. Anstatt eines Mehrheitsvotums kombinieren wir die einzelnen Modelle hier allerdings mit einem Logistischen Modell, wodurch die Modelle in ihrer Qualität gewichtet werden und das Gesamtergebnis besser wird.

from sklearn.ensemble import StackingClassifier

clf_STK = StackingClassifier(estimators=[('lr', LogisticRegression()),('dt',DecisionTreeClassifier())], final_estimator=LogisticRegression())
clf_STK.fit(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]], egywth_train.EV_HT_740_IS_ON.values)

---------------------------------------------------------------------------
ImportError                               Traceback (most recent call last)
File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/__init__.py:24
     23 try:
---> 24     from . import multiarray
     25 except ImportError as exc:

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/multiarray.py:10
      9 import functools
---> 10 from . import overrides
     11 from . import _multiarray_umath

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/overrides.py:8
      7 from .._utils._inspect import getargspec
----> 8 from numpy.core._multiarray_umath import (
      9     add_docstring,  _get_implementing_args, _ArrayFunctionDispatcher)
     12 ARRAY_FUNCTIONS = set()

ImportError: dlopen(/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/_multiarray_umath.cpython-311-darwin.so, 0x0002): Library not loaded: @rpath/libgfortran.5.dylib
  Referenced from: <342C6FCD-A261-33D7-B978-626161CFD49B> /opt/miniconda3/envs/lehre/lib/libopenblas.0.dylib
  Reason: tried: '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/usr/local/lib/libgfortran.5.dylib' (no such file), '/usr/lib/libgfortran.5.dylib' (no such file, not in dyld cache)

During handling of the above exception, another exception occurred:

ImportError                               Traceback (most recent call last)
File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__init__.py:130
    129 try:
--> 130     from numpy.__config__ import show as show_config
    131 except ImportError as e:

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__config__.py:4
      3 from enum import Enum
----> 4 from numpy.core._multiarray_umath import (
      5     __cpu_features__,
      6     __cpu_baseline__,
      7     __cpu_dispatch__,
      8 )
     10 __all__ = ["show"]

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/__init__.py:50
     27     msg = """
     28 
     29 IMPORTANT: PLEASE READ THIS FOR ADVICE ON HOW TO SOLVE THIS ISSUE!
   (...)
     48 """ % (sys.version_info[0], sys.version_info[1], sys.executable,
     49         __version__, exc)
---> 50     raise ImportError(msg)
     51 finally:

ImportError: 

IMPORTANT: PLEASE READ THIS FOR ADVICE ON HOW TO SOLVE THIS ISSUE!

Importing the numpy C-extensions failed. This error can happen for
many reasons, often due to issues with your setup or how NumPy was
installed.

We have compiled some common reasons and troubleshooting tips at:

    https://numpy.org/devdocs/user/troubleshooting-importerror.html

Please note and check the following:

  * The Python version is: Python3.11 from "/opt/miniconda3/envs/lehre/bin/python"
  * The NumPy version is: "1.26.4"

and make sure that they are the versions you expect.
Please carefully study the documentation linked above for further help.

Original error was: dlopen(/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/_multiarray_umath.cpython-311-darwin.so, 0x0002): Library not loaded: @rpath/libgfortran.5.dylib
  Referenced from: <342C6FCD-A261-33D7-B978-626161CFD49B> /opt/miniconda3/envs/lehre/lib/libopenblas.0.dylib
  Reason: tried: '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/usr/local/lib/libgfortran.5.dylib' (no such file), '/usr/lib/libgfortran.5.dylib' (no such file, not in dyld cache)


The above exception was the direct cause of the following exception:

ImportError                               Traceback (most recent call last)
Cell In[49], line 1
----> 1 from sklearn.ensemble import StackingClassifier
      3 clf_STK = StackingClassifier(estimators=[('lr', LogisticRegression()),('dt',DecisionTreeClassifier())], final_estimator=LogisticRegression())
      4 clf_STK.fit(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]], egywth_train.EV_HT_740_IS_ON.values)

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/sklearn/__init__.py:73
     62 # `_distributor_init` allows distributors to run custom init code.
     63 # For instance, for the Windows wheel, this is used to pre-load the
     64 # vcomp shared library runtime for OpenMP embedded in the sklearn/.libs
   (...)
     67 # later is linked to the OpenMP runtime to make it possible to introspect
     68 # it and importing it first would fail if the OpenMP dll cannot be found.
     69 from . import (  # noqa: F401 E402
     70     __check_build,
     71     _distributor_init,
     72 )
---> 73 from .base import clone  # noqa: E402
     74 from .utils._show_versions import show_versions  # noqa: E402
     76 _submodules = [
     77     "calibration",
     78     "cluster",
   (...)
    114     "compose",
    115 ]

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/sklearn/base.py:14
     11 import warnings
     12 from collections import defaultdict
---> 14 import numpy as np
     16 from . import __version__
     17 from ._config import config_context, get_config

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__init__.py:135
    131 except ImportError as e:
    132     msg = """Error importing numpy: you should not try to import numpy from
    133     its source directory; please exit the numpy source tree, and relaunch
    134     your python interpreter from there."""
--> 135     raise ImportError(msg) from e
    137 __all__ = [
    138     'exceptions', 'ModuleDeprecationWarning', 'VisibleDeprecationWarning',
    139     'ComplexWarning', 'TooHardError', 'AxisError']
    141 # mapping of {name: (value, deprecation_msg)}

ImportError: Error importing numpy: you should not try to import numpy from
        its source directory; please exit the numpy source tree, and relaunch
        your python interpreter from there.

egywth_train["pred_STK"] = clf_STK.predict(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]])
print('Train Accuracy: {:.2f}'.format(accuracy_score(egywth_train.EV_HT_740_IS_ON.values, egywth_train.pred_STK)))

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[50], line 1
----> 1 egywth_train["pred_STK"] = clf_STK.predict(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]])
      2 print('Train Accuracy: {:.2f}'.format(accuracy_score(egywth_train.EV_HT_740_IS_ON.values, egywth_train.pred_STK)))

NameError: name 'clf_STK' is not defined

egywth_test["pred_STK"] = clf_STK.predict(egywth_test[["SDK", "NM", "VPM", "TMK", "Weekday"]])
print('Test Accuracy: {:.2f}'.format(accuracy_score(egywth_test.EV_HT_740_IS_ON.values, egywth_test.pred_STK)))

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[51], line 1
----> 1 egywth_test["pred_STK"] = clf_STK.predict(egywth_test[["SDK", "NM", "VPM", "TMK", "Weekday"]])
      2 print('Test Accuracy: {:.2f}'.format(accuracy_score(egywth_test.EV_HT_740_IS_ON.values, egywth_test.pred_STK)))

NameError: name 'clf_STK' is not defined

Voting

Beim Voting kombinieren wir mehrere Basismodelle durch Mehrheitsabstimmung oder Median/Mittelwertbestimmung.

Wir können zum Beispiel die Basismodelle aus dem Stacking durch Mehrheitsabstimmung kombinieren.

pred=np.zeros(egywth_test.shape[0])
for model in stack:
    pred += model.predict(egywth_test[["SDK", "NM", "VPM", "TMK", "Weekday"]])
egywth_test['pred_stack_vote']= pred > len(forest)/2 # Mehreitsvote

print('Test Accuracy: {:.2f}'.format(accuracy_score(egywth_test.EV_HT_740_IS_ON.values, egywth_test.pred_stack_vote)))

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[52], line 1
----> 1 pred=np.zeros(egywth_test.shape[0])
      2 for model in stack:
      3     pred += model.predict(egywth_test[["SDK", "NM", "VPM", "TMK", "Weekday"]])

NameError: name 'np' is not defined

Auch hierfür bietet sklearn eine Methode an.

from sklearn.ensemble import VotingClassifier
clf_VK = VotingClassifier(estimators=[('lr', LogisticRegression()),('dt',DecisionTreeClassifier())], voting='hard')
clf_VK.fit(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]], egywth_train.EV_HT_740_IS_ON.values)

---------------------------------------------------------------------------
ImportError                               Traceback (most recent call last)
File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/__init__.py:24
     23 try:
---> 24     from . import multiarray
     25 except ImportError as exc:

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/multiarray.py:10
      9 import functools
---> 10 from . import overrides
     11 from . import _multiarray_umath

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/overrides.py:8
      7 from .._utils._inspect import getargspec
----> 8 from numpy.core._multiarray_umath import (
      9     add_docstring,  _get_implementing_args, _ArrayFunctionDispatcher)
     12 ARRAY_FUNCTIONS = set()

ImportError: dlopen(/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/_multiarray_umath.cpython-311-darwin.so, 0x0002): Library not loaded: @rpath/libgfortran.5.dylib
  Referenced from: <342C6FCD-A261-33D7-B978-626161CFD49B> /opt/miniconda3/envs/lehre/lib/libopenblas.0.dylib
  Reason: tried: '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/usr/local/lib/libgfortran.5.dylib' (no such file), '/usr/lib/libgfortran.5.dylib' (no such file, not in dyld cache)

During handling of the above exception, another exception occurred:

ImportError                               Traceback (most recent call last)
File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__init__.py:130
    129 try:
--> 130     from numpy.__config__ import show as show_config
    131 except ImportError as e:

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__config__.py:4
      3 from enum import Enum
----> 4 from numpy.core._multiarray_umath import (
      5     __cpu_features__,
      6     __cpu_baseline__,
      7     __cpu_dispatch__,
      8 )
     10 __all__ = ["show"]

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/__init__.py:50
     27     msg = """
     28 
     29 IMPORTANT: PLEASE READ THIS FOR ADVICE ON HOW TO SOLVE THIS ISSUE!
   (...)
     48 """ % (sys.version_info[0], sys.version_info[1], sys.executable,
     49         __version__, exc)
---> 50     raise ImportError(msg)
     51 finally:

ImportError: 

IMPORTANT: PLEASE READ THIS FOR ADVICE ON HOW TO SOLVE THIS ISSUE!

Importing the numpy C-extensions failed. This error can happen for
many reasons, often due to issues with your setup or how NumPy was
installed.

We have compiled some common reasons and troubleshooting tips at:

    https://numpy.org/devdocs/user/troubleshooting-importerror.html

Please note and check the following:

  * The Python version is: Python3.11 from "/opt/miniconda3/envs/lehre/bin/python"
  * The NumPy version is: "1.26.4"

and make sure that they are the versions you expect.
Please carefully study the documentation linked above for further help.

Original error was: dlopen(/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/_multiarray_umath.cpython-311-darwin.so, 0x0002): Library not loaded: @rpath/libgfortran.5.dylib
  Referenced from: <342C6FCD-A261-33D7-B978-626161CFD49B> /opt/miniconda3/envs/lehre/lib/libopenblas.0.dylib
  Reason: tried: '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/usr/local/lib/libgfortran.5.dylib' (no such file), '/usr/lib/libgfortran.5.dylib' (no such file, not in dyld cache)


The above exception was the direct cause of the following exception:

ImportError                               Traceback (most recent call last)
Cell In[53], line 1
----> 1 from sklearn.ensemble import VotingClassifier
      2 clf_VK = VotingClassifier(estimators=[('lr', LogisticRegression()),('dt',DecisionTreeClassifier())], voting='hard')
      3 clf_VK.fit(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]], egywth_train.EV_HT_740_IS_ON.values)

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/sklearn/__init__.py:73
     62 # `_distributor_init` allows distributors to run custom init code.
     63 # For instance, for the Windows wheel, this is used to pre-load the
     64 # vcomp shared library runtime for OpenMP embedded in the sklearn/.libs
   (...)
     67 # later is linked to the OpenMP runtime to make it possible to introspect
     68 # it and importing it first would fail if the OpenMP dll cannot be found.
     69 from . import (  # noqa: F401 E402
     70     __check_build,
     71     _distributor_init,
     72 )
---> 73 from .base import clone  # noqa: E402
     74 from .utils._show_versions import show_versions  # noqa: E402
     76 _submodules = [
     77     "calibration",
     78     "cluster",
   (...)
    114     "compose",
    115 ]

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/sklearn/base.py:14
     11 import warnings
     12 from collections import defaultdict
---> 14 import numpy as np
     16 from . import __version__
     17 from ._config import config_context, get_config

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__init__.py:135
    131 except ImportError as e:
    132     msg = """Error importing numpy: you should not try to import numpy from
    133     its source directory; please exit the numpy source tree, and relaunch
    134     your python interpreter from there."""
--> 135     raise ImportError(msg) from e
    137 __all__ = [
    138     'exceptions', 'ModuleDeprecationWarning', 'VisibleDeprecationWarning',
    139     'ComplexWarning', 'TooHardError', 'AxisError']
    141 # mapping of {name: (value, deprecation_msg)}

ImportError: Error importing numpy: you should not try to import numpy from
        its source directory; please exit the numpy source tree, and relaunch
        your python interpreter from there.

egywth_train["pred_VK"] = clf_VK.predict(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]])
print('Train Accuracy: {:.2f}'.format(accuracy_score(egywth_train.EV_HT_740_IS_ON.values, egywth_train.pred_VK)))

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[54], line 1
----> 1 egywth_train["pred_VK"] = clf_VK.predict(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]])
      2 print('Train Accuracy: {:.2f}'.format(accuracy_score(egywth_train.EV_HT_740_IS_ON.values, egywth_train.pred_VK)))

NameError: name 'clf_VK' is not defined

egywth_test["pred_VK"] = clf_VK.predict(egywth_test[["SDK", "NM", "VPM", "TMK", "Weekday"]])
print('Test Accuracy: {:.2f}'.format(accuracy_score(egywth_test.EV_HT_740_IS_ON.values, egywth_test.pred_VK)))

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[55], line 1
----> 1 egywth_test["pred_VK"] = clf_VK.predict(egywth_test[["SDK", "NM", "VPM", "TMK", "Weekday"]])
      2 print('Test Accuracy: {:.2f}'.format(accuracy_score(egywth_test.EV_HT_740_IS_ON.values, egywth_test.pred_VK)))

NameError: name 'clf_VK' is not defined

Support Vector Machines

Support Vector Machines (SVMs) sind ein weiteres Modell, das zur Klassifikation und Regression verwendet werden kann. Sie sind besonders gut geeignet für Aufgaben, bei denen die Datenpunkte durch eine nichtlineare Entscheidungsgrenze getrennt werden können (Bei linearen Grenzen kann man logistische Modelle nutzen, bei scharfen Grenzen Entscheidungsbäume). SVM zielt darauf ab, die beste Trennlinie (oder Hyperebene in höheren Dimensionen) zu finden, die die Datenpunkte verschiedener Klassen mit maximalem Abstand trennen.

Lineare SVM

Für ein einfaches binäres Klassifizierungsproblem mit zwei Klassen \( y_i \in \{-1, 1\} \) und Datenpunkten \( \bar{x}_i \in \mathbb{R}^n \), suchen wir eine Hyperebene, die die Daten trennt. Bei linearen SVM wir diese Hyperebene durch ein lineares Modell beschrieben:

\[ b + \bar{w} \cdot \bar{x}= 0 \]

Dabei ist \( \bar{w} \) der Normalenvektor zur Hyperebene und \(b\) ist der Bias (Verschiebungsterm). Damit sind lineare Kernel dem logistischen Regressionsmodell sehr ähnlich und zeigt eine ähnliche lineare Entscheidungsgrenze.

Der Hyperebene teilt den Raum so, dass das Vorzeichen

• positiv ist mit \(b + \bar{w} \cdot \bar x_i \geq 0\) für \(y_i=1\)

• negativ ist mit \(b + \bar{w} \cdot \bar x_i \lt 0\) für \(y_i=-1\)

Der Abstand zwischen den beiden nächsten Punkten beider Klassen (die als Support Vectors bezeichnet werden) und dem Hyperebene wird als Margin bezeichnet. Die SVM maximiert diese Margin, was gleichbedeutend mit der Minimierung von \(|\bar{w}|\) ist. Die Optimierungsaufgabe lautet daher:

\[ \min_{\bar{w}, b} \frac{1}{2} \|\bar{w}\|^2 \]

unter den Nebenbedingungen

\[ \quad y_i (b + \bar{w} \cdot \bar{x}_i) \geq 1, \, \forall i. \]

Der Kerneltrick bei nicht-lineare SVM

Für nicht-lineare Probleme können wir die Datenpunkte in einen höherdimensionalen Raum transformieren, wo sie linear trennbar sind, so dass wir dort weiterhin ein Lineares Model nutzen können. Diese Transformation wird durch den sogenannten Kerneltrick erreicht. Ein Kernel ist eine Funktion \( K(\bar{x}_i, \bar{x}_j) \), die das Skalarprodukt der Datenpunkte im höherdimensionalen Raum berechnet, ohne dass die Transformation explizit durchgeführt werden muss. Beliebte Kernelfunktionen sind:

• Linearkern: \( K(\bar{x}_i, \bar{x}_j) = \bar{x}_i \cdot \bar{x}_j \)

• Polynomkern: \( K(\bar{x}_i, \bar{x}_j) = (\bar{x}_i \cdot \bar{x}_j + 1)^d \)

• RBF-Kern (Radial Basis Function): \( K(\bar{x}_i, \bar{x}_j) = \exp(-\gamma \|\bar{x}_i - \bar{x}_j\|^2) \)

Damit ist der Kernel vom Prinzip vergleichbar mit der Transferfunktion in einem GAM-Model, mit dem Unterschied, dass der Kernel das Skalarprodukt transformiert.

Um den Kernelfunktionen Rechnung zu tragen, ändert sich das Optimierungsproblem zu:

\[ \min_{\bar{w}, b} \frac{1}{2} \|\bar{w}\|^2 + C \sum_{i=1}^n \xi_i \]

unter den Nebenbedingungen

\[ y_i (b + \bar{w} \cdot \phi( b + \bar{x}_i)) \geq 1 - \xi_i, \, \xi_i \geq 0, \, \forall i \]

Dabei ist \( \phi(\bar{x}) \) die Abbildung in den höheren dimensionsunabhängigen Raum und \( \xi_i \) sind die Schlupfvariablen. Diese sind notwendig, um bei nicht vollständig linear trennbaren Daten, die Fehlklassifikationen zu modellieren (gleich dem Fehlerterm \(\varepsilon\)).

Das Optimierungsproblems wird als Duales Problem gelöst. Die duale Formulierung ermöglicht es, die Berechnungen nur in Form von Skalarprodukten (oder Kernelfunktionen) durchzuführen:

\[ \max_{\alpha} \sum_{i=1}^n \alpha_i - \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \alpha_i \alpha_j y_i y_j K(\bar{x}_i, \bar{x}_j) \]

mit den Lagrange-Multiplikatoren \( \alpha_i \) und unter den Nebenbedingungen

\[ \quad 0 \leq \alpha_i \leq C, \, \sum_{i=1}^n \alpha_i y_i = 0. \]

Die Entscheidungsfunktion im Dualraum wird durch die Lagrange-Multiplikatoren und Kernelfunktion ausgedrückt:

\[ \bar y = \text{sign}\left( b + \sum_{i=1}^n \alpha_i y_i K(\bar{x}_i, \bar{x}) \right). \]

SVM in SciKit

Wir betrachten als illustratives Beispiel einmal ein zufällig erzeugtes Yin-Yang-Muster. Dies ist ein 2D-Datensatz, bei dem verschiedene Punkte unterschiedlich eingefärbt sind, und die Aufgabe besteht darin, die richtige Farbe basierend auf dem Punkt zu vorhersagen. Es handelt sich also um eine grundlegendes Klassifikationsproblem. Um die Aufgabe jedoch hinreichend komplex zu gestalten, führen wir die Farben in einem Spiralmuster ein. Wir erstellen die Daten wie folgt:

import plotly.express as px

np.random.seed(33)
N = 1000  # Anzahl der Punkte
X1 = np.random.normal(size=N)
X2 = np.random.normal(size=N) 
X = np.column_stack((X1, X2))
y = X1 + X2 - 1.7*np.sin(1.2*(X1 - X2)) + np.random.normal(scale=0.5, size=N) > 0

fig=px.scatter(x=X1, y=X2, color=y, width=600, height=600, color_discrete_sequence=["black", "white"])
fig.update_traces(marker_line=dict(width=.3, color="black"))
fig.show()

---------------------------------------------------------------------------
ImportError                               Traceback (most recent call last)
Cell In[56], line 1
----> 1 import plotly.express as px
      3 np.random.seed(33)
      4 N = 1000  # Anzahl der Punkte

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/plotly/express/__init__.py:9
      7 pd = optional_imports.get_module("pandas")
      8 if pd is None:
----> 9     raise ImportError(
     10         """\
     11 Plotly express requires pandas to be installed."""
     12     )
     14 from ._imshow import imshow
     15 from ._chart_types import (  # noqa: F401
     16     scatter,
     17     scatter_3d,
   (...)
     54     density_mapbox,
     55 )

ImportError: Plotly express requires pandas to be installed.

Das Bild zeigt weiße und schwarze Punkte, die ein unvollkommenes Yin-Yang-Muster mit einer unscharfen Grenze zwischen den Klassen bilden.

Der SVM-Klassifikator SVC ist im Paket sklearn.svm implementiert. Der Konstruktor der Klasse akzeptiert eine Anzahl von Argumenten, von denen die wichtigsten kernel sind, um verschiedene Kernel auszuwählen, sowie die entsprechenden Parameter für verschiedene Kernel, z.B. degree für den Polynomgrad und gamma für den radialen Skalierungsparameter.

Die Erstellung, das Fitting und Scoring des Modells folgen dem bekannten Muster

from sklearn.svm import SVC

m = SVC(kernel="linear")
_ = m.fit(X, y)
m.score(X, y)  # on training data

---------------------------------------------------------------------------
ImportError                               Traceback (most recent call last)
File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/__init__.py:24
     23 try:
---> 24     from . import multiarray
     25 except ImportError as exc:

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/multiarray.py:10
      9 import functools
---> 10 from . import overrides
     11 from . import _multiarray_umath

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/overrides.py:8
      7 from .._utils._inspect import getargspec
----> 8 from numpy.core._multiarray_umath import (
      9     add_docstring,  _get_implementing_args, _ArrayFunctionDispatcher)
     12 ARRAY_FUNCTIONS = set()

ImportError: dlopen(/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/_multiarray_umath.cpython-311-darwin.so, 0x0002): Library not loaded: @rpath/libgfortran.5.dylib
  Referenced from: <342C6FCD-A261-33D7-B978-626161CFD49B> /opt/miniconda3/envs/lehre/lib/libopenblas.0.dylib
  Reason: tried: '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/usr/local/lib/libgfortran.5.dylib' (no such file), '/usr/lib/libgfortran.5.dylib' (no such file, not in dyld cache)

During handling of the above exception, another exception occurred:

ImportError                               Traceback (most recent call last)
File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__init__.py:130
    129 try:
--> 130     from numpy.__config__ import show as show_config
    131 except ImportError as e:

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__config__.py:4
      3 from enum import Enum
----> 4 from numpy.core._multiarray_umath import (
      5     __cpu_features__,
      6     __cpu_baseline__,
      7     __cpu_dispatch__,
      8 )
     10 __all__ = ["show"]

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/__init__.py:50
     27     msg = """
     28 
     29 IMPORTANT: PLEASE READ THIS FOR ADVICE ON HOW TO SOLVE THIS ISSUE!
   (...)
     48 """ % (sys.version_info[0], sys.version_info[1], sys.executable,
     49         __version__, exc)
---> 50     raise ImportError(msg)
     51 finally:

ImportError: 

IMPORTANT: PLEASE READ THIS FOR ADVICE ON HOW TO SOLVE THIS ISSUE!

Importing the numpy C-extensions failed. This error can happen for
many reasons, often due to issues with your setup or how NumPy was
installed.

We have compiled some common reasons and troubleshooting tips at:

    https://numpy.org/devdocs/user/troubleshooting-importerror.html

Please note and check the following:

  * The Python version is: Python3.11 from "/opt/miniconda3/envs/lehre/bin/python"
  * The NumPy version is: "1.26.4"

and make sure that they are the versions you expect.
Please carefully study the documentation linked above for further help.

Original error was: dlopen(/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/_multiarray_umath.cpython-311-darwin.so, 0x0002): Library not loaded: @rpath/libgfortran.5.dylib
  Referenced from: <342C6FCD-A261-33D7-B978-626161CFD49B> /opt/miniconda3/envs/lehre/lib/libopenblas.0.dylib
  Reason: tried: '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/usr/local/lib/libgfortran.5.dylib' (no such file), '/usr/lib/libgfortran.5.dylib' (no such file, not in dyld cache)


The above exception was the direct cause of the following exception:

ImportError                               Traceback (most recent call last)
Cell In[57], line 1
----> 1 from sklearn.svm import SVC
      3 m = SVC(kernel="linear")
      4 _ = m.fit(X, y)

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/sklearn/__init__.py:73
     62 # `_distributor_init` allows distributors to run custom init code.
     63 # For instance, for the Windows wheel, this is used to pre-load the
     64 # vcomp shared library runtime for OpenMP embedded in the sklearn/.libs
   (...)
     67 # later is linked to the OpenMP runtime to make it possible to introspect
     68 # it and importing it first would fail if the OpenMP dll cannot be found.
     69 from . import (  # noqa: F401 E402
     70     __check_build,
     71     _distributor_init,
     72 )
---> 73 from .base import clone  # noqa: E402
     74 from .utils._show_versions import show_versions  # noqa: E402
     76 _submodules = [
     77     "calibration",
     78     "cluster",
   (...)
    114     "compose",
    115 ]

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/sklearn/base.py:14
     11 import warnings
     12 from collections import defaultdict
---> 14 import numpy as np
     16 from . import __version__
     17 from ._config import config_context, get_config

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__init__.py:135
    131 except ImportError as e:
    132     msg = """Error importing numpy: you should not try to import numpy from
    133     its source directory; please exit the numpy source tree, and relaunch
    134     your python interpreter from there."""
--> 135     raise ImportError(msg) from e
    137 __all__ = [
    138     'exceptions', 'ModuleDeprecationWarning', 'VisibleDeprecationWarning',
    139     'ComplexWarning', 'TooHardError', 'AxisError']
    141 # mapping of {name: (value, deprecation_msg)}

ImportError: Error importing numpy: you should not try to import numpy from
        its source directory; please exit the numpy source tree, and relaunch
        your python interpreter from there.

Wir erstellen uns eine Visualisierungsfunktion, um die Grenzen besser zu erkennen.

def DBPlot(m, X, y, nGrid = 100):
    x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx1, xx2 = np.meshgrid(np.linspace(x1_min, x1_max, nGrid), 
                           np.linspace(x2_min, x2_max, nGrid))
    XX = np.column_stack((xx1.ravel(), xx2.ravel()))
    hatyy = m.predict(XX).reshape(xx1.shape)
    fig = px.imshow(hatyy, width=600, height=600)
    fig.add_scatter(x=X[:,0]/(x1_max-x1_min)*100+50, y=X[:,1]/(x2_max-x2_min)*100+50, mode="markers", 
        marker=dict(color='white', line=dict(width=.3, color="black")))
    fig.add_scatter(x=X[y,0]/(x1_max-x1_min)*100+50, y=X[y,1]/(x2_max-x2_min)*100+50, mode="markers", 
        marker=dict(color='black'))
    fig.update_coloraxes(showscale=False)
    fig.update_layout(showlegend=False)
    fig.show()

m = SVC(kernel="linear")  # linear kernel does not have important parameters
_ = m.fit(X, y)
DBPlot(m, X, y)

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[59], line 1
----> 1 m = SVC(kernel="linear")  # linear kernel does not have important parameters
      2 _ = m.fit(X, y)
      3 DBPlot(m, X, y)

NameError: name 'SVC' is not defined

Das Ergebnis ist nicht zu schlecht - es erfasst den groben Unterschied der weißen und schwarzen Punkte, aber kann nicht den Kopf des Yin und Yangs modellieren.

Als nächstes wollen wir dies mit einem Polynomkern zweiten Grades probieren.

m = SVC(kernel="poly", degree=2)
_ = m.fit(X, y)
DBPlot(m, X, y)
m.score(X, y)

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[60], line 1
----> 1 m = SVC(kernel="poly", degree=2)
      2 _ = m.fit(X, y)
      3 DBPlot(m, X, y)

NameError: name 'SVC' is not defined

Wie Sie sehen können, ist der Polynomkern (2) in der Lage, ein blaues Band auf einem gelben Hintergrund darzustellen. Es ist fraglich, ob dies besser ist als das, was der lineare Kern leisten kann, aber man kann leicht erkennen, dass ein solches Band eine gute Darstellung für andere Arten von Daten wäre.

Als nächstes, repliziere das oben Genannte mit einem Grad-3-Kernel:

m = SVC(kernel="poly", degree=3)
_ = m.fit(X, y)
DBPlot(m, X, y)
m.score(X, y)

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[61], line 1
----> 1 m = SVC(kernel="poly", degree=3)
      2 _ = m.fit(X, y)
      3 DBPlot(m, X, y)

NameError: name 'SVC' is not defined

Und schließlich mit einem radialen Kernel:

m = SVC(kernel="rbf", gamma=1)
_ = m.fit(X, y)
DBPlot(m, X, y)
m.score(X, y)

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[62], line 1
----> 1 m = SVC(kernel="rbf", gamma=1)
      2 _ = m.fit(X, y)
      3 DBPlot(m, X, y)

NameError: name 'SVC' is not defined

Vergleichen wir diese mit den Entscheidungsbäumen und Ensamble-Modellen so sehen wir, dass diese den Trainingsdatensatz inklusiver der Ausnahmen gut erlernen, dadurch allerdings keine stetigen Grenzen erkennen.

m = DecisionTreeClassifier()
_ = m.fit(X, y)
DBPlot(m, X, y)
m.score(X, y)

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[63], line 1
----> 1 m = DecisionTreeClassifier()
      2 _ = m.fit(X, y)
      3 DBPlot(m, X, y)

NameError: name 'DecisionTreeClassifier' is not defined

m = RandomForestClassifier()
_ = m.fit(X, y)
DBPlot(m, X, y)
m.score(X, y)

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[64], line 1
----> 1 m = RandomForestClassifier()
      2 _ = m.fit(X, y)
      3 DBPlot(m, X, y)

NameError: name 'RandomForestClassifier' is not defined

Als nächstes testen wir die SVM-Modelle einmal auf der Energievorhersage.

clf_SVCL = SVC(kernel="linear")
clf_SVCL.fit(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]], egywth_train.EV_HT_740_IS_ON.values)

egywth_train["pred_SVCL"] = clf_SVCL.predict(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]])
print('Train Accuracy: {:.2f}'.format(accuracy_score(egywth_train.EV_HT_740_IS_ON.values, egywth_train.pred_SVCL)))
egywth_test["pred_SVCL"] = clf_SVCL.predict(egywth_test[["SDK", "NM", "VPM", "TMK", "Weekday"]])
print('Test Accuracy: {:.2f}'.format(accuracy_score(egywth_test.EV_HT_740_IS_ON.values, egywth_test.pred_SVCL)))

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[65], line 1
----> 1 clf_SVCL = SVC(kernel="linear")
      2 clf_SVCL.fit(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]], egywth_train.EV_HT_740_IS_ON.values)
      4 egywth_train["pred_SVCL"] = clf_SVCL.predict(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]])

NameError: name 'SVC' is not defined

clf_SVCP = SVC(kernel="poly", degree=3)
clf_SVCP.fit(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]], egywth_train.EV_HT_740_IS_ON.values)

egywth_train["pred_SVCP"] = clf_SVCP.predict(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]])
print('Train Accuracy: {:.2f}'.format(accuracy_score(egywth_train.EV_HT_740_IS_ON.values, egywth_train.pred_SVCL)))
egywth_test["pred_SVCP"] = clf_SVCP.predict(egywth_test[["SDK", "NM", "VPM", "TMK", "Weekday"]])
print('Test Accuracy: {:.2f}'.format(accuracy_score(egywth_test.EV_HT_740_IS_ON.values, egywth_test.pred_SVCP)))

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[66], line 1
----> 1 clf_SVCP = SVC(kernel="poly", degree=3)
      2 clf_SVCP.fit(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]], egywth_train.EV_HT_740_IS_ON.values)
      4 egywth_train["pred_SVCP"] = clf_SVCP.predict(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]])

NameError: name 'SVC' is not defined

clf_SVCR = SVC(kernel="rbf", gamma=1)
clf_SVCR.fit(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]], egywth_train.EV_HT_740_IS_ON.values)

egywth_train["pred_SVCR"] = clf_SVCR.predict(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]])
print('Train Accuracy: {:.2f}'.format(accuracy_score(egywth_train.EV_HT_740_IS_ON.values, egywth_train.pred_SVCR)))
egywth_test["pred_SVCR"] = clf_SVCR.predict(egywth_test[["SDK", "NM", "VPM", "TMK", "Weekday"]])
print('Test Accuracy: {:.2f}'.format(accuracy_score(egywth_test.EV_HT_740_IS_ON.values, egywth_test.pred_SVCR)))

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[67], line 1
----> 1 clf_SVCR = SVC(kernel="rbf", gamma=1)
      2 clf_SVCR.fit(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]], egywth_train.EV_HT_740_IS_ON.values)
      4 egywth_train["pred_SVCR"] = clf_SVCR.predict(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]])

NameError: name 'SVC' is not defined

Die Vorhersagequalität dieser Modelle ist nicht sehr hoch. Das liegt daran, dass Trennlinien im Datensatz nicht gegeben sind. In solchen Fällen sind Entscheidungsbäume und Ensambles besser geeignet, obwohl sie wie gezeigt schnell zum Overfitting neigen. Dennoch gehören SVM mit zu den beliebtesten Modellen. Deshalb empfiehlt es sich immer vorher ein Scatter-Diagramm mit der Zielklasse als Farbcode zu erstellen, um zu sehen, ob sich klare Grenzen erkennen lassen.

px.scatter_matrix(egywth, dimensions=["SDK", "NM", "VPM", "TMK"], opacity=.2, color="EV_HT_740_IS_ON")

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[68], line 1
----> 1 px.scatter_matrix(egywth, dimensions=["SDK", "NM", "VPM", "TMK"], opacity=.2, color="EV_HT_740_IS_ON")

NameError: name 'px' is not defined

Regressionsbäume und Regressions-Ensemble-Modelle

Wir können Entscheidungsbäume und Ensemble-Modelle auch als Regressionsmodell benutzen. Hierbei soll nicht eine spezifische Klasse einer kategorischen Variable vorhergesagt werden, sondern eine numerische Variable. Das Prinzip der Regressionsvarianten ist das gleiche wie beiden diskreten Modellen, nur werden die Ergebnisse nicht durch Mehrheitsabstimmung kombiniert, sondern linear addiert.

Vergleichen wir die oben genannten Varianten einmal in ihren Regressions-Varianten und sagen den Energieverbrauch ES_Lab wie bei den Regressionsmodellen voraus.

from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor, StackingRegressor, VotingRegressor
from sklearn.linear_model import LinearRegression
from sklearn.svm import SVR
from sklearn.metrics import mean_squared_error, root_mean_squared_error, r2_score
import time 

reg_models=[("Linear Model", LinearRegression()),
            ("Decision Tree", DecisionTreeRegressor()),
            ("Random Forest", RandomForestRegressor()),
            ("Gradient Boost", GradientBoostingRegressor()),
            ("XGBoost", xgb.XGBRegressor()),
            ("Stack", StackingRegressor(estimators=[('lm', LinearRegression()),('dt',DecisionTreeRegressor())])),
            ("Vote", VotingRegressor(estimators=[('lm', LinearRegression()),('dt',DecisionTreeRegressor())])),
            ("BoostStack", StackingRegressor(estimators=[('lm', LinearRegression()),('rf',RandomForestRegressor()),('xgb',xgb.XGBRegressor())])),
            ("SVM_l", SVR(kernel="linear")),
            ("SVM_p", SVR(kernel="poly")),
            ("SVM_r", SVR(kernel="rbf")),
            ("SVMStack", StackingRegressor(estimators=[('lm', LinearRegression()),('svm',SVR(kernel="linear")),('rf',RandomForestRegressor()),('xgb',xgb.XGBRegressor())])),]

resdf=[]
for mtype,model in reg_models:
    starttime=time.time()
    model.fit(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]], egywth_train.ES_Lab.values)
    fittime=time.time()
    pred_train = model.predict(egywth_train[["SDK", "NM", "VPM", "TMK", "Weekday"]])
    pred_test  = model.predict(egywth_test[["SDK", "NM", "VPM", "TMK", "Weekday"]])
    predtime=time.time()
    resdf.append({"type":mtype,
                  "train.MSE":mean_squared_error(egywth_train.ES_Lab.values, pred_train),
                  "train.RMSE":root_mean_squared_error(egywth_train.ES_Lab.values, pred_train),
                  "train.R2":r2_score(egywth_train.ES_Lab.values, pred_train),
                  "test.MSE":mean_squared_error(egywth_test.ES_Lab.values, pred_test),
                  "test.RMSE":root_mean_squared_error(egywth_test.ES_Lab.values, pred_test),
                  "test.R2":r2_score(egywth_test.ES_Lab.values, pred_test),
                  "fittime":fittime-starttime,
                  "predtime":predtime-fittime})

---------------------------------------------------------------------------
ImportError                               Traceback (most recent call last)
File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/__init__.py:24
     23 try:
---> 24     from . import multiarray
     25 except ImportError as exc:

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/multiarray.py:10
      9 import functools
---> 10 from . import overrides
     11 from . import _multiarray_umath

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/overrides.py:8
      7 from .._utils._inspect import getargspec
----> 8 from numpy.core._multiarray_umath import (
      9     add_docstring,  _get_implementing_args, _ArrayFunctionDispatcher)
     12 ARRAY_FUNCTIONS = set()

ImportError: dlopen(/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/_multiarray_umath.cpython-311-darwin.so, 0x0002): Library not loaded: @rpath/libgfortran.5.dylib
  Referenced from: <342C6FCD-A261-33D7-B978-626161CFD49B> /opt/miniconda3/envs/lehre/lib/libopenblas.0.dylib
  Reason: tried: '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/usr/local/lib/libgfortran.5.dylib' (no such file), '/usr/lib/libgfortran.5.dylib' (no such file, not in dyld cache)

During handling of the above exception, another exception occurred:

ImportError                               Traceback (most recent call last)
File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__init__.py:130
    129 try:
--> 130     from numpy.__config__ import show as show_config
    131 except ImportError as e:

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__config__.py:4
      3 from enum import Enum
----> 4 from numpy.core._multiarray_umath import (
      5     __cpu_features__,
      6     __cpu_baseline__,
      7     __cpu_dispatch__,
      8 )
     10 __all__ = ["show"]

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/__init__.py:50
     27     msg = """
     28 
     29 IMPORTANT: PLEASE READ THIS FOR ADVICE ON HOW TO SOLVE THIS ISSUE!
   (...)
     48 """ % (sys.version_info[0], sys.version_info[1], sys.executable,
     49         __version__, exc)
---> 50     raise ImportError(msg)
     51 finally:

ImportError: 

IMPORTANT: PLEASE READ THIS FOR ADVICE ON HOW TO SOLVE THIS ISSUE!

Importing the numpy C-extensions failed. This error can happen for
many reasons, often due to issues with your setup or how NumPy was
installed.

We have compiled some common reasons and troubleshooting tips at:

    https://numpy.org/devdocs/user/troubleshooting-importerror.html

Please note and check the following:

  * The Python version is: Python3.11 from "/opt/miniconda3/envs/lehre/bin/python"
  * The NumPy version is: "1.26.4"

and make sure that they are the versions you expect.
Please carefully study the documentation linked above for further help.

Original error was: dlopen(/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/_multiarray_umath.cpython-311-darwin.so, 0x0002): Library not loaded: @rpath/libgfortran.5.dylib
  Referenced from: <342C6FCD-A261-33D7-B978-626161CFD49B> /opt/miniconda3/envs/lehre/lib/libopenblas.0.dylib
  Reason: tried: '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/core/../../../../libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/opt/miniconda3/envs/lehre/bin/../lib/libgfortran.5.dylib' (duplicate LC_RPATH '@loader_path'), '/usr/local/lib/libgfortran.5.dylib' (no such file), '/usr/lib/libgfortran.5.dylib' (no such file, not in dyld cache)


The above exception was the direct cause of the following exception:

ImportError                               Traceback (most recent call last)
Cell In[69], line 1
----> 1 from sklearn.tree import DecisionTreeRegressor
      2 from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor, StackingRegressor, VotingRegressor
      3 from sklearn.linear_model import LinearRegression

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/sklearn/__init__.py:73
     62 # `_distributor_init` allows distributors to run custom init code.
     63 # For instance, for the Windows wheel, this is used to pre-load the
     64 # vcomp shared library runtime for OpenMP embedded in the sklearn/.libs
   (...)
     67 # later is linked to the OpenMP runtime to make it possible to introspect
     68 # it and importing it first would fail if the OpenMP dll cannot be found.
     69 from . import (  # noqa: F401 E402
     70     __check_build,
     71     _distributor_init,
     72 )
---> 73 from .base import clone  # noqa: E402
     74 from .utils._show_versions import show_versions  # noqa: E402
     76 _submodules = [
     77     "calibration",
     78     "cluster",
   (...)
    114     "compose",
    115 ]

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/sklearn/base.py:14
     11 import warnings
     12 from collections import defaultdict
---> 14 import numpy as np
     16 from . import __version__
     17 from ._config import config_context, get_config

File /opt/miniconda3/envs/lehre/lib/python3.11/site-packages/numpy/__init__.py:135
    131 except ImportError as e:
    132     msg = """Error importing numpy: you should not try to import numpy from
    133     its source directory; please exit the numpy source tree, and relaunch
    134     your python interpreter from there."""
--> 135     raise ImportError(msg) from e
    137 __all__ = [
    138     'exceptions', 'ModuleDeprecationWarning', 'VisibleDeprecationWarning',
    139     'ComplexWarning', 'TooHardError', 'AxisError']
    141 # mapping of {name: (value, deprecation_msg)}

ImportError: Error importing numpy: you should not try to import numpy from
        its source directory; please exit the numpy source tree, and relaunch
        your python interpreter from there.

resdf=pd.DataFrame(resdf)
resdf

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[70], line 1
----> 1 resdf=pd.DataFrame(resdf)
      2 resdf

NameError: name 'pd' is not defined

Hier sehen wir, wieder das Overfitten der Entscheidungsbäume im Trainingsdatensatz, aber schlechter als Regressionsmodelle abschneiden im Testdatensatz. Wir sehen auch, dass die Regressions-Ensamble-Modelle sogar besser abschneiden als die klassischen linearen Regressionsmodelle. Das liegt daran das die zugrundeliegenden Entscheidungsbäume vom Normalen linearen Verhalten abweichende Ausnahmen besser erfassen können. Die Stacking Varianten schneiden zum Teil am besten ab, aber weisen auch die größten Trainingszeiten auf.